Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 57, 58, 59 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, khoa học, giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập Toán 8.
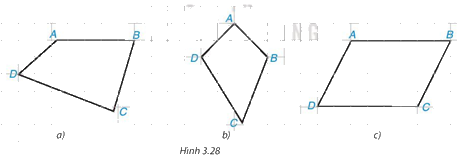
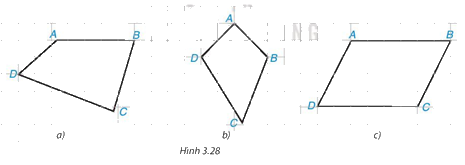
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Video hướng dẫn giải
Hãy nêu các tính chất của hình bình hành mà em đã biết.
Phương pháp giải:
Dựa vào hình bình hành để nêu các tính chất.
Lời giải chi tiết:
Các tính chất của hình bình hành mà em đã biết:
- Hai cặp cạnh đối song song.
- Hai cặp cạnh đối bằng nhau.
Video hướng dẫn giải
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Phương pháp giải:
Quan sát hình 3.28
Lời giải chi tiết:
Tứ giác trong Hình 3.28c là hình bình hành vì:
Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình.
Ta thấy AB = CD; AD = BC.
Video hướng dẫn giải
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Phương pháp giải:
Vẽ hình theo đề bài và chứng minh tứ giác ABCD có các cặp cạnh đối song song với nhau nên ABCD là hình bình hành.
Lời giải chi tiết:
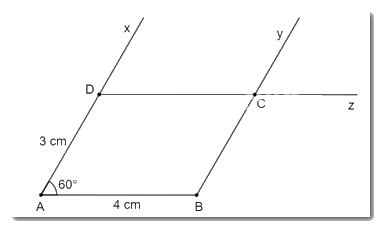
Giả sử hình bình hành ABCD có AD = 3cm, AB = 4 cm và \(\widehat {BA{\rm{D}}} = {60^o}\)
Cách vẽ:
- Vẽ cạnh AB = 4 cm.
- Vẽ \(\widehat {{\rm{BAx}}} = {60^o}\). Trên tia Ax lấy điểm D sao cho AD = 3cm.
- Kẻ By // AD, Dz // BC. Hai tia By và Dz cắt nhau tại C, ta được hình bình hành ABCD.
Hình vẽ được là hình bình hành vì có hai cặp cạnh đối song song (AB // CD, AD // BC).
Video hướng dẫn giải
Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn thẳng AM.
Phương pháp giải:
Chứng minh APMN là hình bình hành.
Lời giải chi tiết:
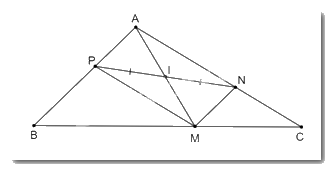
Xét tứ giác APMN có:
• MN // AP (vì MN // AB)
• MP // AN (vì MP // AC)
Do đó tứ giác APMN là hình bình hành.
Hình bình hành APMN có I là trung điểm của đoạn AP.
Do đó I là trung điểm của đoạn thẳng AM (đpcm).
Video hướng dẫn giải
Cho hình bình hành ABCD (H.3.30).
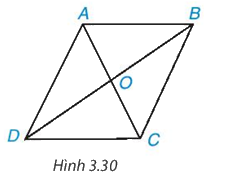
a) Chứng minh ∆ABC = ∆CDA.
Từ đó suy ra AB = CD, AD = BC và \(\widehat {ABC} = \widehat {C{\rm{D}}A}\)
b) Chứng minh ∆ABD = ∆CDB. Từ đó suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\)
c) Gọi giao điểm của hai đường chéo AC, BD là O. Chứng minh ∆AOB = ∆COD. Từ đó suy ra OA = OC, OB = OD.
Phương pháp giải:
Sử dụng các tính chất của hình bình hành
Lời giải chi tiết:
a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra \(\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {BCA} = \widehat {DAC}\)(hai góc so le trong).
Xét ∆ABC và ∆CDA có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
Cạnh AC chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); \(\widehat {ABC} = \widehat {C{\rm{D}}A}\) (hai góc tương ứng).
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\) (hai góc tương ứng).
c) Xét ∆AOB và ∆COD có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
AB = CD (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).
Video hướng dẫn giải
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Phương pháp giải:
Quan sát hình 3.28
Lời giải chi tiết:
Tứ giác trong Hình 3.28c là hình bình hành vì:
Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình.
Ta thấy AB = CD; AD = BC.
Video hướng dẫn giải
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Phương pháp giải:
Vẽ hình theo đề bài và chứng minh tứ giác ABCD có các cặp cạnh đối song song với nhau nên ABCD là hình bình hành.
Lời giải chi tiết:
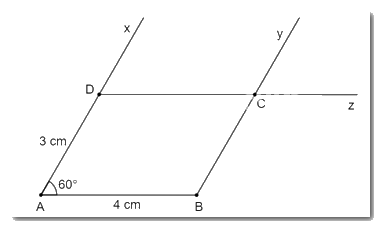
Giả sử hình bình hành ABCD có AD = 3cm, AB = 4 cm và \(\widehat {BA{\rm{D}}} = {60^o}\)
Cách vẽ:
- Vẽ cạnh AB = 4 cm.
- Vẽ \(\widehat {{\rm{BAx}}} = {60^o}\). Trên tia Ax lấy điểm D sao cho AD = 3cm.
- Kẻ By // AD, Dz // BC. Hai tia By và Dz cắt nhau tại C, ta được hình bình hành ABCD.
Hình vẽ được là hình bình hành vì có hai cặp cạnh đối song song (AB // CD, AD // BC).
Video hướng dẫn giải
Hãy nêu các tính chất của hình bình hành mà em đã biết.
Phương pháp giải:
Dựa vào hình bình hành để nêu các tính chất.
Lời giải chi tiết:
Các tính chất của hình bình hành mà em đã biết:
- Hai cặp cạnh đối song song.
- Hai cặp cạnh đối bằng nhau.
Video hướng dẫn giải
Cho hình bình hành ABCD (H.3.30).
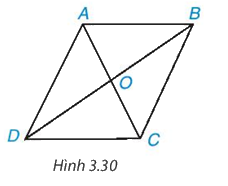
a) Chứng minh ∆ABC = ∆CDA.
Từ đó suy ra AB = CD, AD = BC và \(\widehat {ABC} = \widehat {C{\rm{D}}A}\)
b) Chứng minh ∆ABD = ∆CDB. Từ đó suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\)
c) Gọi giao điểm của hai đường chéo AC, BD là O. Chứng minh ∆AOB = ∆COD. Từ đó suy ra OA = OC, OB = OD.
Phương pháp giải:
Sử dụng các tính chất của hình bình hành
Lời giải chi tiết:
a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra \(\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {BCA} = \widehat {DAC}\)(hai góc so le trong).
Xét ∆ABC và ∆CDA có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
Cạnh AC chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); \(\widehat {ABC} = \widehat {C{\rm{D}}A}\) (hai góc tương ứng).
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\) (hai góc tương ứng).
c) Xét ∆AOB và ∆COD có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
AB = CD (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).
Video hướng dẫn giải
Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn thẳng AM.
Phương pháp giải:
Chứng minh APMN là hình bình hành.
Lời giải chi tiết:
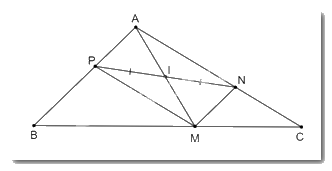
Xét tứ giác APMN có:
• MN // AP (vì MN // AB)
• MP // AN (vì MP // AC)
Do đó tứ giác APMN là hình bình hành.
Hình bình hành APMN có I là trung điểm của đoạn AP.
Do đó I là trung điểm của đoạn thẳng AM (đpcm).
Video hướng dẫn giải
Tròn khẳng định: Hình thang cân có hai cạnh bên bằng nhau. Ngược lại, hình thang có hai cạnh bên bằng nhau thì nó là hình thang cân.
Vuông lại cho rằng: Tròn sai rồi!
Có trường hợp hình thang có hai cạnh bên bằng nhau nhưng nó lại là hình bình hành mà không phải là hình thang cân.
Theo em, bạn nào đúng? Vì sao?
Phương pháp giải:
Dựa vào tính chất của hình thang
Lời giải chi tiết:
Khẳng định của bạn Vuông là đúng.
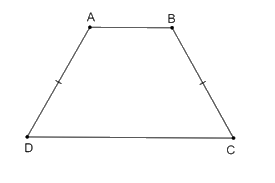
Trường hợp 1: Hình thang có hai cạnh bên bằng nhau nhưng không song song với nhau thì hình thang đó là hình thang cân.
Hình minh họa:
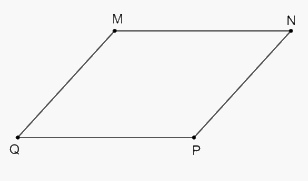
Trường hợp 2: Hình thang có hai cạnh bên bằng nhau và song song với nhau thì hình thang đó là hình bình hành.
Hình minh họa:
Video hướng dẫn giải
Tròn khẳng định: Hình thang cân có hai cạnh bên bằng nhau. Ngược lại, hình thang có hai cạnh bên bằng nhau thì nó là hình thang cân.
Vuông lại cho rằng: Tròn sai rồi!
Có trường hợp hình thang có hai cạnh bên bằng nhau nhưng nó lại là hình bình hành mà không phải là hình thang cân.
Theo em, bạn nào đúng? Vì sao?
Phương pháp giải:
Dựa vào tính chất của hình thang
Lời giải chi tiết:
Khẳng định của bạn Vuông là đúng.
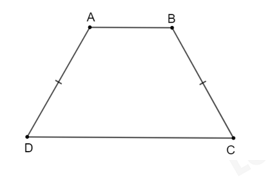
Trường hợp 1: Hình thang có hai cạnh bên bằng nhau nhưng không song song với nhau thì hình thang đó là hình thang cân.
Hình minh họa:
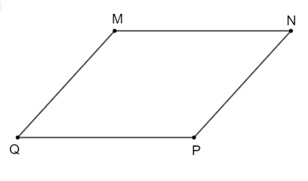
Trường hợp 2: Hình thang có hai cạnh bên bằng nhau và song song với nhau thì hình thang đó là hình bình hành.
Hình minh họa:
Mục 1 của chương trình Toán 8 tập 1 Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này giúp học sinh củng cố các khái niệm, định lý và kỹ năng đã học, đồng thời rèn luyện khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia đa thức. Để giải quyết bài tập này, học sinh cần nắm vững các quy tắc về phép toán trên đa thức, bao gồm quy tắc dấu ngoặc, quy tắc nhân đơn thức với đa thức, quy tắc chia đa thức cho đơn thức, và quy tắc chia đa thức cho đa thức.
Bài tập này yêu cầu học sinh phân tích đa thức thành nhân tử bằng các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, và nhóm đa thức. Việc phân tích đa thức thành nhân tử giúp học sinh đơn giản hóa biểu thức, tìm nghiệm của đa thức, và giải các phương trình đa thức.
Bài tập này yêu cầu học sinh rút gọn biểu thức đại số bằng cách sử dụng các quy tắc về phép toán trên đa thức và phân thức đại số. Việc rút gọn biểu thức đại số giúp học sinh đơn giản hóa biểu thức, tìm giá trị của biểu thức, và giải các bài toán liên quan đến biểu thức đại số.
| Biểu thức | Rút gọn |
|---|---|
| (x + 1)2 - (x - 1)2 | 4x |
| (x2 - 1)/(x + 1) | x - 1 |
Để giải các bài tập trong mục 1 trang 57, 58, 59 SGK Toán 8 tập 1 Kết nối tri thức một cách hiệu quả, học sinh cần:
Hãy dành thời gian ôn tập lý thuyết và làm bài tập đầy đủ để nắm vững kiến thức Toán 8 tập 1. Đừng ngần ngại hỏi giáo viên hoặc bạn bè nếu gặp khó khăn trong quá trình học tập. Chúc các em học tốt!
Sách giáo khoa Toán 8 tập 1 - Kết nối tri thức
Sách bài tập Toán 8 tập 1 - Kết nối tri thức
Các trang web học toán online uy tín