Bài 4.12 trang 86 SGK Toán 8 tập 1 thuộc chương 4: Các tứ giác đặc biệt. Bài tập này yêu cầu học sinh vận dụng kiến thức về hình thang cân, tính chất đường trung bình của hình thang để giải quyết. Giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 8, Toán 7, Toán 6, Toán 9, Toán 10, Toán 11, Toán 12.
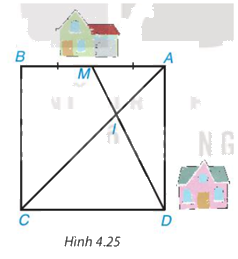
Nhà bạn Mai ở vị trí M,
Đề bài
Nhà bạn Mai ở vị trí M, nhà bạn Dung ở vị trí D (Hình 4.25), biết rằng tứ giác ABCD là hình vuông và M là trung điểm của AB. Hai bạn đi bộ với cùng một vận tốc trên con đường MD để đến điểm I. Bạn Mai xuất phát lúc 7h. Hỏi bạn Dung xuất phát lúc mấy giờ để gặp bạn Mai lúc 7h30 tại điểm I?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định quãng đường mỗi bạn phải đi để đến I dựa vào tính chất đường phân giác trong tam giác
Tính thời gian bạn Mai đi, khi đó ta xác định được vận tốc (giả sử vận tốc hai bạn là như nhau).
Ta biết quãng đường và vận tốc của bạn Dung, tính thời gian để bạn Dung đến điểm I lúc 7h30.
Lời giải chi tiết
Theo đề bài, ABCD là hình vuông nên AB = AD và AC là tia phân giác của \(\widehat {BA{\rm{D}}}\)
Vì M là trung điểm của AB nên \(AM = BM = \dfrac{1}{2}AB = \dfrac{1}{2}A{\rm{D}}\) hay \(\dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{1}{2}\)
Vì AC là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay AI là tia phân giác của \(\widehat {MA{\rm{D}}}\), áp dụng tính chất đường phân giác trong tam giác ADM, ta có:
\(\dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{{IM}}{{I{\rm{D}}}} = \dfrac{1}{2}\) suy ra ID = 2IM.
Giả sử vận tốc đi bộ của bạn Mai và bạn Dung đều bằng nhau.
Theo đề bài, I là địa điểm gặp nhau nên bạn Mai đi theo quãng đường MI, bạn Dung đi theo quãng đường DI.
Vì quãng đường bạn Dung đi gấp 2 lần quãng đường bạn Mai đi và vận tốc đi bộ của hai bạn đều bằng nhau (giả sử) nên thời gian bạn Dung đi gấp 2 lần thời gian bạn Mai đi thì hai bạn mới gặp nhau tại địa điểm I.
Bạn Dung gặp bạn Mai lúc 7h30 nên thời gian bạn Mai đi trên quãng đường MI là:
7h30 – 7h = 30 phút.
Khi đó, thời gian bạn Dung đi là 1h. Do đó, bạn Dung xuất phát từ lúc:
7h30 – 1h = 6h30.
Vậy bạn Dung xuất phát lúc 6h30 để gặp bạn Mai lúc 7h30 tại điểm I.
Bài 4.12 trang 86 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình thang cân và đường trung bình của hình thang. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và tính chất sau:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho. Sau đó, phân tích đề bài để tìm ra mối liên hệ giữa các yếu tố và lựa chọn phương pháp giải phù hợp. Thông thường, bài tập về hình thang cân sẽ yêu cầu tính độ dài các cạnh, góc, đường chéo hoặc chứng minh một tính chất nào đó.
(Nội dung lời giải chi tiết bài tập 4.12 sẽ được trình bày tại đây, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng. Ví dụ:)
Đề bài: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = 5cm. Tính độ dài đường trung bình của hình thang.
Lời giải:
Ngoài bài 4.12, còn rất nhiều bài tập tương tự về hình thang cân và đường trung bình của hình thang. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân và đường trung bình của hình thang, học sinh có thể tự giải các bài tập sau:
Bài 4.12 trang 86 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hình thang cân và đường trung bình của hình thang. Bằng cách nắm vững các kiến thức và phương pháp giải đã trình bày, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ có thêm công cụ hỗ trợ trong quá trình học tập và ôn luyện môn Toán 8.