Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 77, 78 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải các bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho Hình 4.2, em hãy thực hiện các hoạt động sau: Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số (dfrac{{AB}}{{C{rm{D}}}})
Video hướng dẫn giải
So sánh hai tỉ số tìm được trong hai hoạt động trên
Phương pháp giải:
Dựa vào tỉ số của hai hoạt động 1, 2.
Lời giải chi tiết:
Tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\) tìm được ở Hoạt động 1 và hoạt động 2 bằng nhau và đều bằng \(\dfrac{1}{3}\)
Video hướng dẫn giải
Tính tỉ số của các đoạn thẳng có độ dài như sau:
a) MN = 3 cm và PQ = 9 cm.
b) EF = 25 cm và HK = 10 dm.
Phương pháp giải:
Dựa vào độ dài các đoạn thẳng đã cho ta tính tỉ số (đổi các đơn vị để cùng đơn vị đo)
Lời giải chi tiết:
a) Tỉ số của các đoạn thẳng được tính như sau: \(\dfrac{{MN}}{{PQ}} = \dfrac{3}{9} = \dfrac{1}{3};\dfrac{{PQ}}{{MN}} = \dfrac{9}{3} = 3\)
Vậy: \(\dfrac{{MN}}{{PQ}} = \dfrac{1}{3};\dfrac{{PQ}}{{MN}} = 3\)
b) Đổi 10dm = 100cm
Tỉ số của các đoạn thẳng được tính như sau: \(\dfrac{{EF}}{{HK}} = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{HK}}{{EF}} = \dfrac{{100}}{{25}} = 4\)
Vậy: \(\dfrac{{EF}}{{HK}} = \dfrac{1}{4};\dfrac{{HK}}{{EF}} = 4\)
Video hướng dẫn giải
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
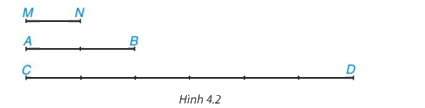
Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Phương pháp giải:
Quan sát hình 4.2 chọn MN = 1 (đvđd) khi đó tính được độ dài AB và CD và tình tỉnh số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Lời giải chi tiết:
Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).
Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).
Do đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Vậy AB = 2 (đvđd); CD = 6 (đvđd); \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{1}{3}\)
Video hướng dẫn giải
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
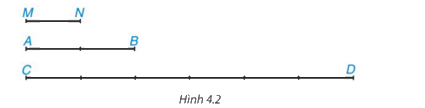
Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Phương pháp giải:
Quan sát hình 4.2 và dùng thước thẳng để đo độ dài đoạn thẳng AB và CD
Lời giải chi tiết:
Đo độ dài các đoạn thẳng, ta được: AB = 4,8 cm; CD = 14,4 cm.
Khi đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{{4,8}}{{14,4}} = \dfrac{1}{3}\)
Video hướng dẫn giải
Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta vẽ một đường thẳng song song với BC, cắt A tại C’ (H.4.4
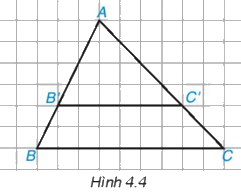
Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:
a) \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
b) \(\dfrac{{AB'}}{{B'B}}\) và \(\dfrac{{AC'}}{{C'C}}\)
c) \(\dfrac{{B'B}}{{AB}}\) và \(\dfrac{{C'C}}{{AC}}\)
Phương pháp giải:
Quan sát hình 4.4
Lời giải chi tiết:
a) Từ hình vẽ ta thấy: \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{4}{6} = \dfrac{2}{3}\)
Do đó, \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\)
b) Từ hình vẽ, ta thấy: \(\dfrac{{AB'}}{{B'B}} = \dfrac{4}{2} = \dfrac{2}{1};\dfrac{{AC'}}{{C'C}} = \dfrac{4}{2} = \dfrac{2}{1}\)
Vậy: \(\dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\)
c) Từ hình vẽ ta thấy: \(\dfrac{{B'B}}{{AB}} = \dfrac{2}{6} = \dfrac{1}{3};\dfrac{{C'C}}{{AC}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Do đó: \(\dfrac{{B'B}}{{AB}} = \dfrac{{C'C}}{{AC}}\)
Video hướng dẫn giải
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
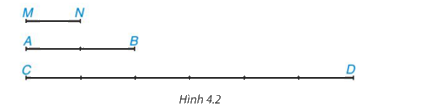
Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Phương pháp giải:
Quan sát hình 4.2 chọn MN = 1 (đvđd) khi đó tính được độ dài AB và CD và tình tỉnh số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Lời giải chi tiết:
Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).
Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).
Do đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Vậy AB = 2 (đvđd); CD = 6 (đvđd); \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{1}{3}\)
Video hướng dẫn giải
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
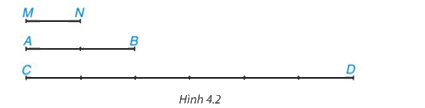
Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Phương pháp giải:
Quan sát hình 4.2 và dùng thước thẳng để đo độ dài đoạn thẳng AB và CD
Lời giải chi tiết:
Đo độ dài các đoạn thẳng, ta được: AB = 4,8 cm; CD = 14,4 cm.
Khi đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{{4,8}}{{14,4}} = \dfrac{1}{3}\)
Video hướng dẫn giải
So sánh hai tỉ số tìm được trong hai hoạt động trên
Phương pháp giải:
Dựa vào tỉ số của hai hoạt động 1, 2.
Lời giải chi tiết:
Tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\) tìm được ở Hoạt động 1 và hoạt động 2 bằng nhau và đều bằng \(\dfrac{1}{3}\)
Video hướng dẫn giải
Tính tỉ số của các đoạn thẳng có độ dài như sau:
a) MN = 3 cm và PQ = 9 cm.
b) EF = 25 cm và HK = 10 dm.
Phương pháp giải:
Dựa vào độ dài các đoạn thẳng đã cho ta tính tỉ số (đổi các đơn vị để cùng đơn vị đo)
Lời giải chi tiết:
a) Tỉ số của các đoạn thẳng được tính như sau: \(\dfrac{{MN}}{{PQ}} = \dfrac{3}{9} = \dfrac{1}{3};\dfrac{{PQ}}{{MN}} = \dfrac{9}{3} = 3\)
Vậy: \(\dfrac{{MN}}{{PQ}} = \dfrac{1}{3};\dfrac{{PQ}}{{MN}} = 3\)
b) Đổi 10dm = 100cm
Tỉ số của các đoạn thẳng được tính như sau: \(\dfrac{{EF}}{{HK}} = \dfrac{{25}}{{100}} = \dfrac{1}{4};\dfrac{{HK}}{{EF}} = \dfrac{{100}}{{25}} = 4\)
Vậy: \(\dfrac{{EF}}{{HK}} = \dfrac{1}{4};\dfrac{{HK}}{{EF}} = 4\)
Video hướng dẫn giải
Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta vẽ một đường thẳng song song với BC, cắt A tại C’ (H.4.4
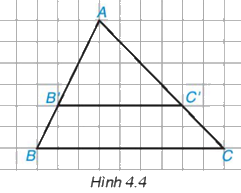
Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:
a) \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
b) \(\dfrac{{AB'}}{{B'B}}\) và \(\dfrac{{AC'}}{{C'C}}\)
c) \(\dfrac{{B'B}}{{AB}}\) và \(\dfrac{{C'C}}{{AC}}\)
Phương pháp giải:
Quan sát hình 4.4
Lời giải chi tiết:
a) Từ hình vẽ ta thấy: \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{4}{6} = \dfrac{2}{3}\)
Do đó, \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\)
b) Từ hình vẽ, ta thấy: \(\dfrac{{AB'}}{{B'B}} = \dfrac{4}{2} = \dfrac{2}{1};\dfrac{{AC'}}{{C'C}} = \dfrac{4}{2} = \dfrac{2}{1}\)
Vậy: \(\dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\)
c) Từ hình vẽ ta thấy: \(\dfrac{{B'B}}{{AB}} = \dfrac{2}{6} = \dfrac{1}{3};\dfrac{{C'C}}{{AC}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Do đó: \(\dfrac{{B'B}}{{AB}} = \dfrac{{C'C}}{{AC}}\)
Mục 1 trang 77, 78 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng thu gọn đa thức, tìm bậc của đa thức, và thực hiện các phép cộng, trừ đa thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các kiến thức nâng cao hơn trong chương trình Toán 8.
Bài 1 yêu cầu học sinh thu gọn các đa thức đã cho. Để thu gọn một đa thức, ta cần thực hiện các bước sau:
Ví dụ, để thu gọn đa thức 3x2 + 2x - x2 + 5x - 3, ta thực hiện như sau:
Bài 2 yêu cầu học sinh tìm bậc của các đa thức đã thu gọn. Bậc của một đa thức là bậc cao nhất của các hạng tử trong đa thức đó. Ví dụ, đa thức 2x2 + 7x - 3 có bậc là 2.
Bài 3 yêu cầu học sinh thực hiện các phép cộng, trừ đa thức. Để cộng hoặc trừ hai đa thức, ta cần thực hiện các bước sau:
Ví dụ, để cộng hai đa thức A = 2x2 + 7x - 3 và B = -x2 + 5x + 1, ta thực hiện như sau:
Khi giải các bài tập về đa thức, học sinh cần lưu ý những điều sau:
Kiến thức về đa thức có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật. Ví dụ, đa thức được sử dụng để mô tả các hàm số, giải các phương trình, và xây dựng các mô hình toán học.
Để củng cố kiến thức về đa thức, học sinh có thể tự giải thêm các bài tập sau:
Hy vọng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập về đa thức trong SGK Toán 8 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!