Bài 3.8 trang 55 SGK Toán 8 tập 1 thuộc chương 3: Các góc ở hình bình hành. Bài tập này yêu cầu học sinh vận dụng kiến thức về tính chất của hình bình hành, đặc biệt là mối quan hệ giữa các góc đối nhau và các góc kề nhau để giải quyết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.8 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Hình thang cân ABCD (AB // CD, AB < CD) có
Đề bài
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi O là giao điểm của AB và IJ
Chứng minh: Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác \(\widehat {AIB}\)
Suy ra IO là đường trung trực của đoạn thẳng AB.
Suy ra đường thẳng IJ là đường trung trực của đoạn thẳng AB
Lời giải chi tiết
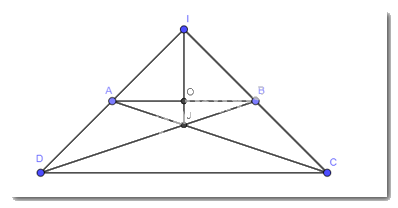
Gọi O là giao điểm của AB và IJ.
Vì ABCD là hình thang cân nên \(\widehat {BA{\rm{D}}} = \widehat {ABC};\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}};A{\rm{D}} = BC, AC = BD\)
Tam giác ICD cân tại I (vì \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)) nên IC = ID.
Xét tam giác ABD và BAC có:
AB chung
AD = BC (cmt)
AC = BD (cmt)
=> ∆ABD = ∆BAC (c.c.c) => \(\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\)
Vì \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}};\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\) nên \(\widehat {J{\rm{D}}C} = \widehat {JC{\rm{D}}}\)
Tam giác JCD cân tại J (vì \(\widehat {J{\rm{D}}C} = \widehat {JC{\rm{D}}}\) ) nên JC = JD.
Xét ∆IJD và ∆IJC có:
IC = ID (chứng minh trên);
\(\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\);
JC = JD (chứng minh trên).
Do đó ∆IJD = ∆IJC (c.g.c).
Suy ra \(\widehat {D{\rm{IJ}}} = \widehat {C{\rm{IJ}}}\) (hai góc tương ứng).
Ta có ID = IC, AD = BC.
Mà ID = AI + AD; IC = IB + BC nên IA = IB.
Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác \(\widehat {AIB}\)
Suy ra IO là đường trung trực của đoạn thẳng AB.
Vậy đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Bài 3.8 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương học về hình bình hành. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Nội dung bài tập 3.8: Bài tập thường yêu cầu tính số đo các góc của hình bình hành khi biết một số góc hoặc mối quan hệ giữa các góc. Đôi khi, bài tập cũng yêu cầu chứng minh một tứ giác là hình bình hành dựa trên các tính chất đã học.
Đề bài (Ví dụ): Cho hình bình hành ABCD, biết góc A = 60 độ. Tính số đo các góc còn lại của hình bình hành.
Lời giải:
Kết luận: Góc B = 120 độ, góc C = 60 độ, góc D = 120 độ.
Ngoài dạng bài tập tính số đo các góc, học sinh có thể gặp các dạng bài tập sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 3.8 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức và các bài tập tương tự. Chúc các em học tốt!
| Khái niệm | Mô tả |
|---|---|
| Hình bình hành | Tứ giác có các cạnh đối song song. |
| Góc đối nhau | Các góc nằm đối diện nhau trong hình bình hành. |
| Góc kề nhau | Các góc nằm cạnh nhau trong hình bình hành. |