Chào mừng bạn đến với bài học về Lý thuyết Đường trung bình của tam giác trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đường trung bình của tam giác, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất và ứng dụng của đường trung bình của tam giác, đồng thời luyện tập thông qua các ví dụ minh họa cụ thể.
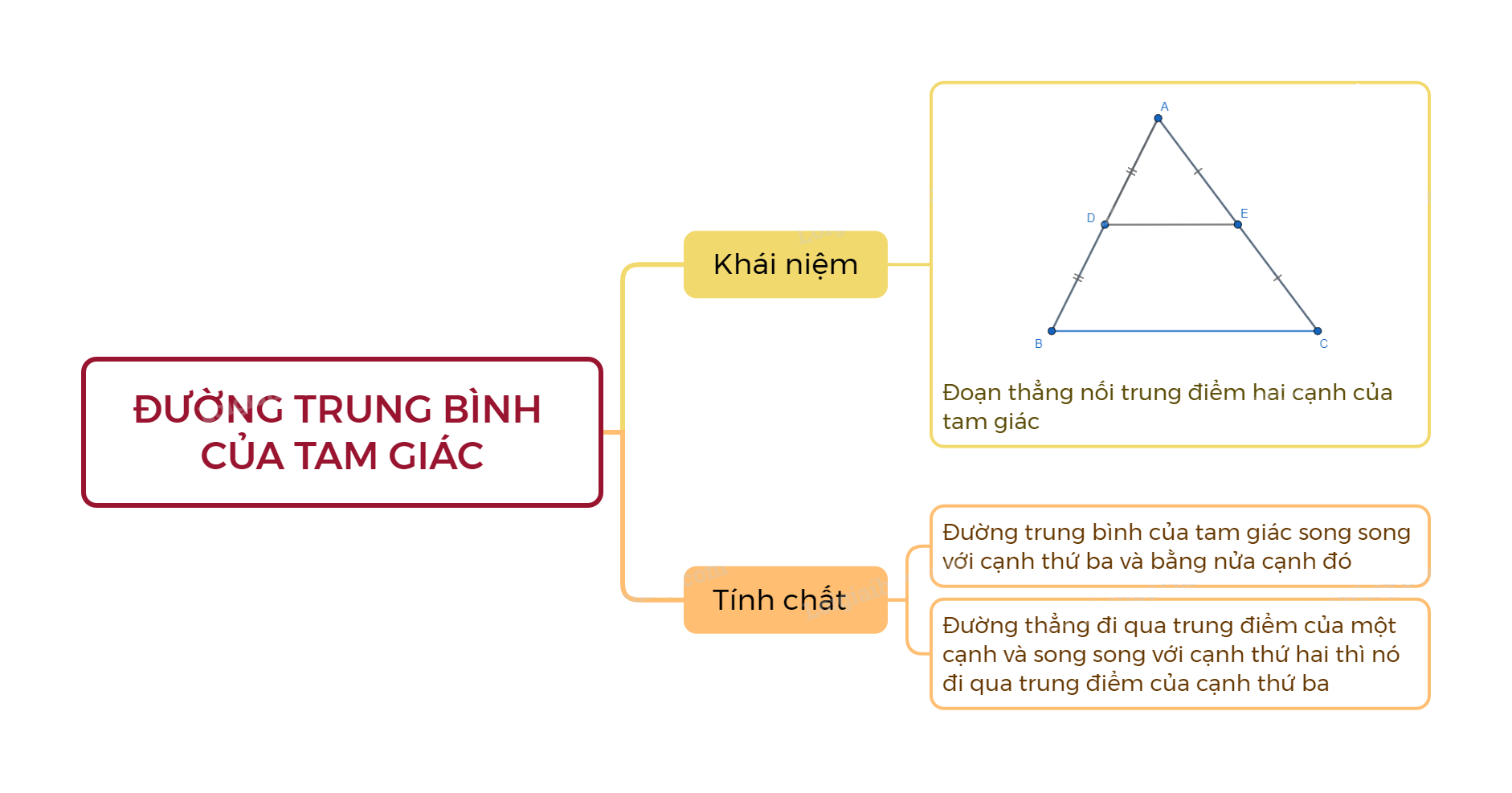
Đường trung bình của tam giác là gì?
1. Khái niệm
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
2. Tính chất
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.
Ví dụ:
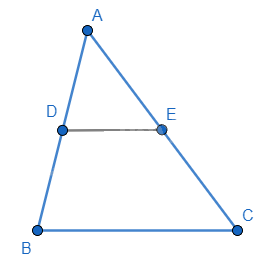
DE là đường trung bình của tam giác ABC, khi đó DE // BC và \(DE = \frac{1}{2}BC\).
Đường trung bình của tam giác là một khái niệm quan trọng trong hình học lớp 8, đóng vai trò nền tảng cho việc giải quyết nhiều bài toán liên quan đến tam giác. Bài viết này sẽ trình bày chi tiết lý thuyết, tính chất và ứng dụng của đường trung bình của tam giác theo chương trình SGK Toán 8 - Kết nối tri thức.
Trong một tam giác, đoạn thẳng nối trung điểm của hai cạnh là đường trung bình của tam giác đó.
Ví dụ: Trong tam giác ABC, nếu M là trung điểm của AB và N là trung điểm của AC, thì MN là đường trung bình của tam giác ABC.
Đường trung bình của tam giác có những tính chất quan trọng sau:
Chứng minh Tính chất 1:
Xét tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Ta có:
Xét hai tam giác AMN và ABC, ta có:
Suy ra, tam giác AMN đồng dạng với tam giác ABC (cạnh - góc - cạnh). Do đó, MN // BC.
Chứng minh Tính chất 2:
Vì tam giác AMN đồng dạng với tam giác ABC (cmt) nên:
MN/BC = AM/AB = 1/2
Suy ra, MN = 1/2 BC.
Đường trung bình của tam giác được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến tính độ dài đoạn thẳng, chứng minh tính song song và đồng dạng của các đoạn thẳng.
Bài 1: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết BC = 10cm. Tính độ dài MN.
Giải: Vì MN là đường trung bình của tam giác ABC nên MN = 1/2 BC = 1/2 * 10cm = 5cm.
Bài 2: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết MN song song với BC. Chứng minh rằng tam giác ABC cân tại A.
Giải: Vì MN song song với BC nên ∠AMN = ∠ABC (so le trong) và ∠ANM = ∠ACB (so le trong). Vì M là trung điểm của AB và N là trung điểm của AC nên AM = MB và AN = NC. Xét hai tam giác AMN và ABC, ta có: ∠AMN = ∠ABC, ∠ANM = ∠ACB và AM = MB. Suy ra, tam giác ABC cân tại A.
Đường trung bình của tam giác không chỉ áp dụng cho tam giác thường mà còn áp dụng cho các loại tam giác đặc biệt như tam giác cân, tam giác vuông, tam giác đều.
Khi giải các bài toán liên quan đến đường trung bình của tam giác, cần chú ý đến việc xác định đúng trung điểm của các cạnh và áp dụng đúng các tính chất của đường trung bình.
Lý thuyết Đường trung bình của tam giác là một kiến thức cơ bản và quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết và tính chất của đường trung bình sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và đầy đủ về chủ đề này.