Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết các bài tập trang 81, 82 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất bài toán, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
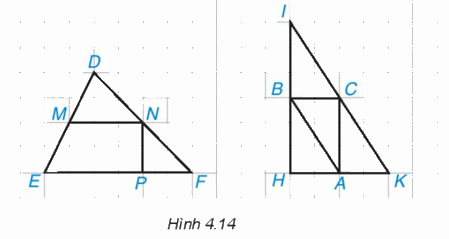
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Video hướng dẫn giải
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Phương pháp giải:
Quan sát hình 4.14
Lời giải chi tiết:
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.
Video hướng dẫn giải
Cho DE là đường trung bình của tam giác ABC (H.4.15)

Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
Phương pháp giải:
Áp dụngđịnh lí Thalès đảo
Lời giải chi tiết:
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).
Video hướng dẫn giải
Cho DE là đường trung bình của tam giác ABC (H.4.15)

Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE = \(\frac{1}{2}\)BC
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hình bình hành.
Sử dụng tính chất của hình bình hành.
Lời giải chi tiết:
Chứng minh tương tự HĐ1, ta có EF // AB.
Xét tam giác DEFB có DE // BF, EF // BD
=> DEFB là hình bình hành.
=> DE = BF (hai cạnh tương ứng)
Mà F là trung điểm của BC => BF = \(\frac{1}{2}\)BC
=> DE = \(\frac{1}{2}\)BC
Video hướng dẫn giải
Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
Phương pháp giải:
Sử dụng tính chất đường trung bình để chứng minh:Tứ giác DECB có DE // BC suy ra tứ giác DECB là hình thang có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
Lời giải chi tiết:
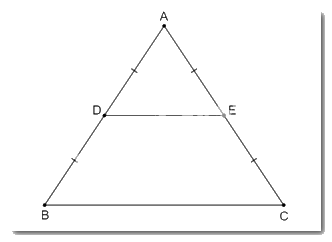
Tam giác ABC cân tại A nên \(\widehat B = \widehat C\)
Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.
Suy ra DE // BC nên tứ giác DECB là hình thang.
Hình thang DECB có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
Video hướng dẫn giải
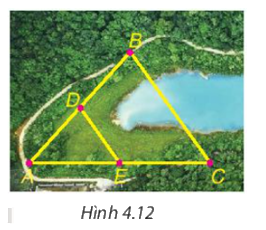
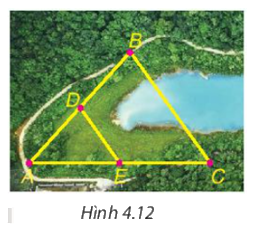
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Phương pháp giải:
Vận dụng tính chất đường trung bình trong tam giác
Lời giải chi tiết:
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó \(DE = \frac{1}{2}BC\) suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.
Video hướng dẫn giải
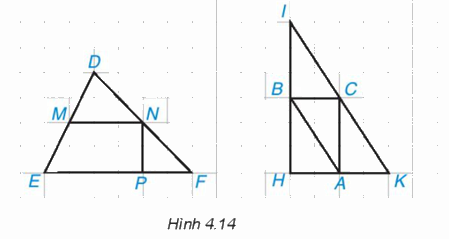
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Phương pháp giải:
Quan sát hình 4.14
Lời giải chi tiết:
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.
Video hướng dẫn giải
Cho DE là đường trung bình của tam giác ABC (H.4.15)
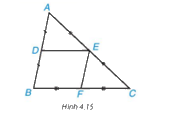
Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
Phương pháp giải:
Áp dụngđịnh lí Thalès đảo
Lời giải chi tiết:
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).
Video hướng dẫn giải
Cho DE là đường trung bình của tam giác ABC (H.4.15)
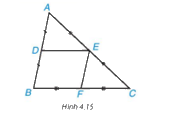
Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE = \(\frac{1}{2}\)BC
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hình bình hành.
Sử dụng tính chất của hình bình hành.
Lời giải chi tiết:
Chứng minh tương tự HĐ1, ta có EF // AB.
Xét tam giác DEFB có DE // BF, EF // BD
=> DEFB là hình bình hành.
=> DE = BF (hai cạnh tương ứng)
Mà F là trung điểm của BC => BF = \(\frac{1}{2}\)BC
=> DE = \(\frac{1}{2}\)BC
Video hướng dẫn giải
Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
Phương pháp giải:
Sử dụng tính chất đường trung bình để chứng minh:Tứ giác DECB có DE // BC suy ra tứ giác DECB là hình thang có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
Lời giải chi tiết:
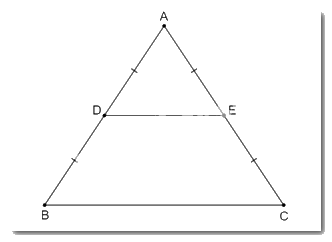
Tam giác ABC cân tại A nên \(\widehat B = \widehat C\)
Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.
Suy ra DE // BC nên tứ giác DECB là hình thang.
Hình thang DECB có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
Video hướng dẫn giải
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Phương pháp giải:
Vận dụng tính chất đường trung bình trong tam giác
Lời giải chi tiết:
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó \(DE = \frac{1}{2}BC\) suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.
Trang 81 và 82 SGK Toán 8 tập 1 Kết nối tri thức tập trung vào các bài tập về đa thức. Cụ thể, các em sẽ được làm quen với các khái niệm như đa thức một biến, bậc của đa thức, các phép toán trên đa thức (cộng, trừ, nhân, chia) và ứng dụng của chúng trong giải toán.
Bài tập này yêu cầu các em thu gọn các đa thức đã cho bằng cách thực hiện các phép cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, các em cần:
Ví dụ: Thu gọn đa thức 3x2 + 2x - 5x2 + x + 1. Ta có:
3x2 + 2x - 5x2 + x + 1 = (3x2 - 5x2) + (2x + x) + 1 = -2x2 + 3x + 1
Bài tập này yêu cầu các em tìm bậc của các đa thức đã cho. Bậc của đa thức là bậc cao nhất của các đơn thức trong đa thức đó. Để tìm bậc của đa thức, các em cần:
Ví dụ: Tìm bậc của đa thức -2x2 + 3x + 1. Ta có:
Bậc của -2x2 là 2, bậc của 3x là 1, bậc của 1 là 0. Vậy bậc của đa thức -2x2 + 3x + 1 là 2.
Bài tập này yêu cầu các em thực hiện các phép cộng, trừ, nhân, chia đa thức. Để thực hiện các phép toán này, các em cần:
Ví dụ: Thực hiện phép cộng hai đa thức (2x2 + 3x - 1) + (x2 - 2x + 2). Ta có:
(2x2 + 3x - 1) + (x2 - 2x + 2) = (2x2 + x2) + (3x - 2x) + (-1 + 2) = 3x2 + x + 1
Đa thức có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ hiểu rõ hơn về các bài tập trang 81, 82 SGK Toán 8 tập 1 Kết nối tri thức và tự tin hơn trong quá trình học tập. Chúc các em học tốt!