Bài học này sẽ giúp học sinh lớp 8 hiểu rõ về mối liên hệ quan trọng giữa xác suất thực nghiệm và xác suất lý thuyết. Chúng ta sẽ cùng nhau khám phá cách thu thập dữ liệu thực tế để ước lượng xác suất và so sánh với kết quả tính toán theo lý thuyết.
Nội dung bài học bám sát chương trình SGK Toán 8 - Kết nối tri thức, cung cấp kiến thức nền tảng vững chắc và các ví dụ minh họa sinh động, giúp học sinh dễ dàng tiếp thu và áp dụng vào giải bài tập.
Xác suất thực nghiệm của biến cố là gì?
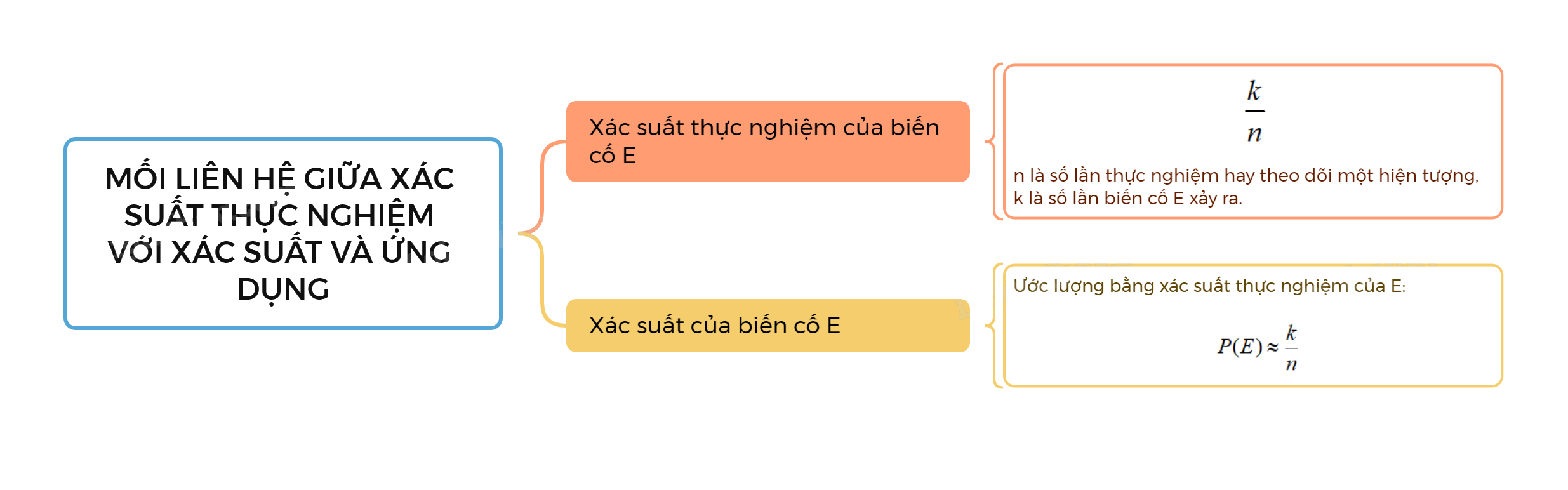
1. Xác suất thực nghiệm của một biến cố
Giả sử trong n lần thực nghiệm hoặc n lần theo dõi (quan sát) một hiện tượng ta thấy biến cố E xảy ra k lần. Khi đó xác suất thực nghiệm của biến cố E bằng \(\frac{k}{n}\), tức là bằng tỉ số giữa số lần xuất hiện của biến cố E và số lần thực hiện thực nghiệm hoặc theo dõi hiện tượng đó.
Ví dụ: Bạn Nam gieo một con xúc xắc 20 lần. Kết quả thu được như sau:
Số chấm | 1 | 2 | 3 | 4 | 5 | 6 |
Số lần | 2 | 4 | 5 | 3 | 2 | 4 |
Gọi A là biến cố “Nam gieo được số chấm lớn hơn 3”. Số chấm lớn hơn 3 là 4, 5 và 6 với số lần gieo được lần lượt là 3, 2 và 4. Khi đó số biến cố A xảy ra là: 3 + 2 + 4 = 9 (lần)
Vậy xác suất thực nghiệm của biến cố A là \(\frac{9}{{20}}\).
2. Mối liên hệ giữa xác suất thực nghiệm với xác suất
Xác suất của biến cố E được ước lượng bằng xác suất thực nghiệm của E:
\(P(E) \approx \frac{k}{n};\)
Trong đó n là số lần thực nghiệm hay theo dõi một hiện tượng, k là số lần biến cố E xảy ra.
Ví dụ: Trong 240 000 trẻ sơ sinh chào đời người ta có 123 120 bé trai.
Số bé gái chào đời là: 240 000 – 123 120 =116 880
Xác suất của biến cố “Trẻ sơ sinh là bé gái” là: \(\frac{{116880}}{{240000}} = \frac{{487}}{{1000}} = 0,487 = 48,7\% \)
Vậy xác suất trẻ sơ sinh là bé gái được ước lượng là 48,7%
Xác suất là một khái niệm quan trọng trong toán học, giúp chúng ta đo lường khả năng xảy ra của một sự kiện. Trong thực tế, việc dự đoán chính xác xác suất của một sự kiện có thể rất khó khăn. Đó là lúc chúng ta cần đến khái niệm xác suất thực nghiệm.
Xác suất thực nghiệm của một sự kiện A, ký hiệu là PTE(A), được tính bằng tỷ lệ giữa số lần sự kiện A xảy ra trong một số lớn các lần thử nghiệm và tổng số lần thử nghiệm. Công thức tính xác suất thực nghiệm là:
PTE(A) = (Số lần sự kiện A xảy ra) / (Tổng số lần thử nghiệm)
Ví dụ: Gieo một đồng xu 100 lần, mặt ngửa xuất hiện 52 lần. Khi đó, xác suất thực nghiệm của sự kiện “mặt ngửa xuất hiện” là:
PTE(mặt ngửa) = 52 / 100 = 0.52
Xác suất lý thuyết của một sự kiện A, ký hiệu là P(A), được tính dựa trên các giả định về tính đối xứng của sự kiện và các điều kiện lý tưởng. Ví dụ, xác suất lý thuyết của sự kiện “mặt ngửa xuất hiện” khi gieo một đồng xu cân đối là 0.5.
Khi số lượng thử nghiệm càng lớn, xác suất thực nghiệm thường tiến gần đến xác suất lý thuyết. Điều này được gọi là Định luật số lớn. Định luật này khẳng định rằng, trong một số lượng lớn các lần thử nghiệm, tần suất xuất hiện của một sự kiện sẽ gần với xác suất lý thuyết của sự kiện đó.
Tuy nhiên, cần lưu ý rằng xác suất thực nghiệm chỉ là một ước lượng của xác suất lý thuyết. Sự khác biệt giữa xác suất thực nghiệm và xác suất lý thuyết có thể xảy ra do các yếu tố ngẫu nhiên hoặc do các giả định lý tưởng không hoàn toàn đúng trong thực tế.
Bài 1: Một hộp chứa 10 quả bóng, trong đó có 6 quả bóng màu đỏ và 4 quả bóng màu xanh. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất thực nghiệm của sự kiện “lấy được quả bóng màu đỏ” sau 50 lần thử nghiệm, biết rằng có 32 lần lấy được quả bóng màu đỏ.
Giải: PTE(quả bóng màu đỏ) = 32 / 50 = 0.64
Bài 2: Gieo một con xúc xắc 6 mặt 100 lần. Kết quả thống kê được như sau:
| Mặt xúc xắc | Số lần xuất hiện |
|---|---|
| 1 | 15 |
| 2 | 18 |
| 3 | 16 |
| 4 | 17 |
| 5 | 19 |
| 6 | 15 |
Tính xác suất thực nghiệm của sự kiện “mặt 5 xuất hiện”.
Giải: PTE(mặt 5) = 19 / 100 = 0.19
Việc hiểu rõ về mối liên hệ giữa xác suất thực nghiệm và xác suất lý thuyết là rất quan trọng trong việc ứng dụng toán học vào thực tế. Hy vọng bài học này đã giúp các em học sinh lớp 8 nắm vững kiến thức và có thể giải quyết các bài toán liên quan đến xác suất một cách hiệu quả.