Chào mừng bạn đến với bài học lý thuyết Hệ số góc của đường thẳng trong chương trình Toán 8 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hệ số góc, giúp bạn hiểu rõ hơn về tính chất của đường thẳng và ứng dụng của nó trong giải toán.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, cách tính hệ số góc, mối liên hệ giữa hệ số góc và độ dốc của đường thẳng, cũng như các bài tập ví dụ minh họa để bạn có thể nắm vững kiến thức một cách dễ dàng.
Hệ số góc của đường thẳng là gì?
1. Hệ số góc của đường thẳng
Góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc \(\alpha \) tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc \(\alpha \))
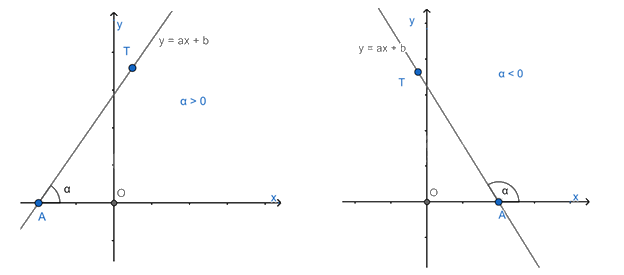
Hệ số góc: Ta gọi a là hệ số góc của đường thẳng y = ax + b (a\( \ne \)0).
Ví dụ: Đường thẳng y = 3x – 1 có hệ số góc là 3;
y = 2 – x có hệ số góc là -1.
2. Nhận biết hai đường thẳng song song
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) song song với nhau khi a = a’; b \( \ne \) b’ và ngược lại.
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) trùng nhau khi a = a’; b = b’ và ngược lại.
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) cắt nhau khi a \( \ne \) a’ và ngược lại.
Ví dụ: Đường thẳng y = -x + 1 và đường thẳng y = -x song song với nhau.
Đường thẳng y = -x + 1 và đường thẳng y = 2x + 1 cắt nhau.
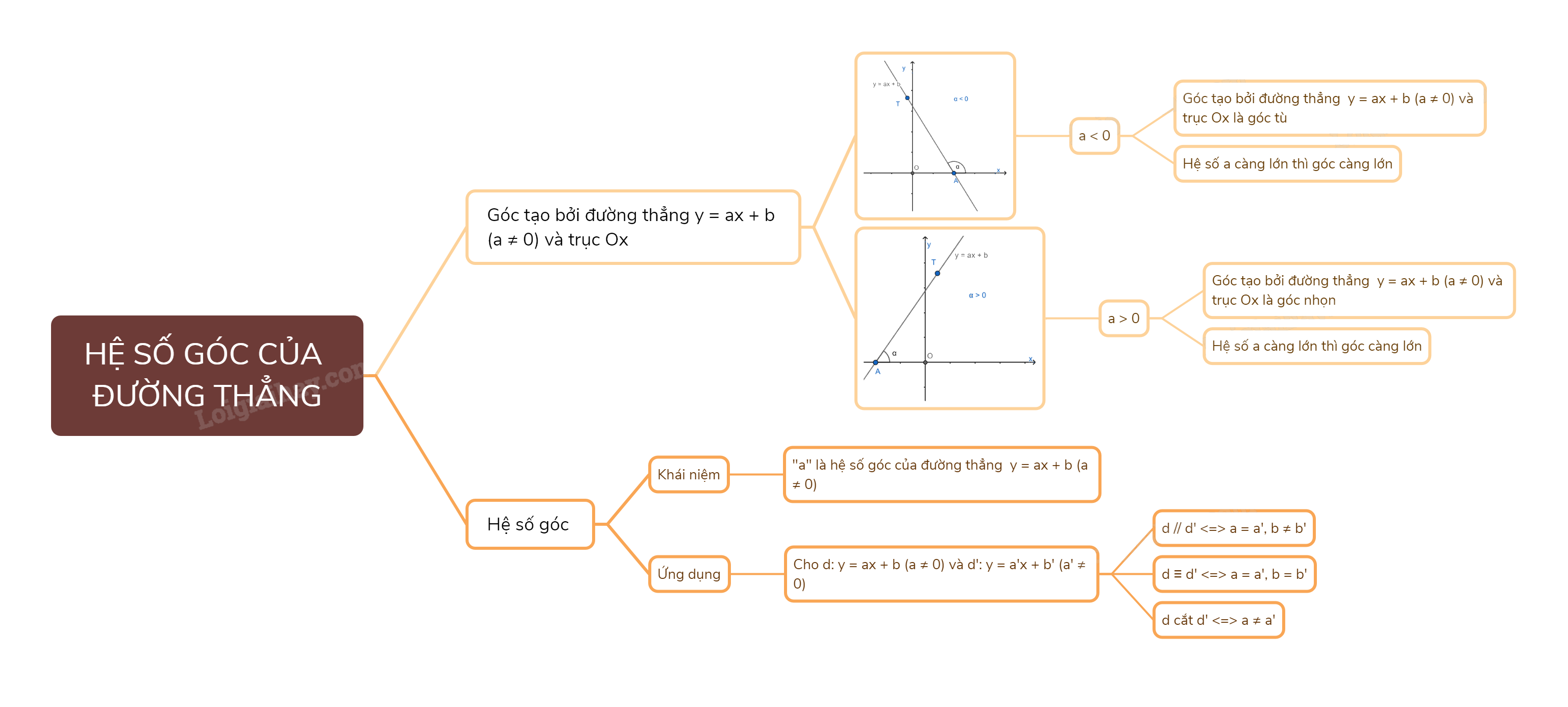
Hệ số góc của đường thẳng là một khái niệm quan trọng trong hình học lớp 8, đặc biệt trong chương trình Kết nối tri thức. Nó đóng vai trò then chốt trong việc xác định độ dốc của đường thẳng và phân tích mối quan hệ giữa các đường thẳng.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình y = ax + b. Hệ số góc của đường thẳng d là số a, ký hiệu là k. Nói cách khác, hệ số góc k thể hiện độ dốc của đường thẳng so với trục hoành.
Có nhiều cách để xác định hệ số góc của một đường thẳng:
Hệ số góc k cho biết độ dốc của đường thẳng:
Cho hai đường thẳng d1: y = a1x + b1 và d2: y = a2x + b2:
Bài 1: Xác định hệ số góc của đường thẳng có phương trình y = -2x + 3.
Giải: Hệ số góc của đường thẳng là k = -2.
Bài 2: Cho hai điểm A(1, 2) và B(3, 6). Xác định hệ số góc của đường thẳng đi qua hai điểm này.
Giải: Hệ số góc k = (6 - 2) / (3 - 1) = 4 / 2 = 2.
Bài 3: Đường thẳng d tạo với trục hoành một góc 45°. Xác định hệ số góc của đường thẳng d.
Giải: Hệ số góc k = tan 45° = 1.
Hệ số góc được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Khi tính hệ số góc từ hai điểm, cần đảm bảo rằng x1 ≠ x2 để tránh việc mẫu số bằng 0. Ngoài ra, cần chú ý đến đơn vị đo góc khi sử dụng công thức k = tan α.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết Hệ số góc của đường thẳng trong chương trình Toán 8 Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải toán một cách hiệu quả.