Chào mừng bạn đến với bài học về Lý thuyết Hình thang cân trong chương trình Toán 8 Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình thang cân, giúp bạn tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân, cũng như các ứng dụng thực tế của nó trong toán học và cuộc sống.
Hình thang là gì?
1. Khái niệm hình thang
Hình thang là tứ giác có hai cạnh đối song song.
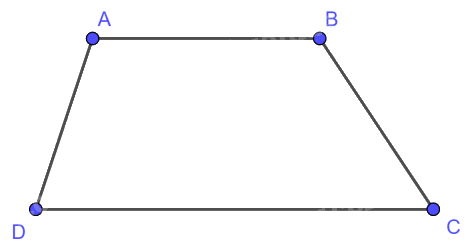
2. Khái niệm hình thang cân
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
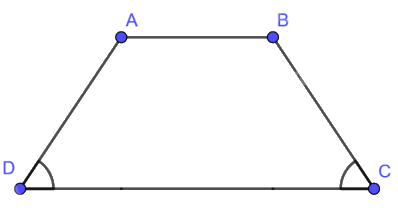
3. Tính chất của hình thang cân
Trong hình thang cân,
- Hai cạnh bên bằng nhau.
- Hai đường chéo bằng nhau.
4. Dấu hiệu nhận biết hình thang cân
- Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.
Ví dụ:
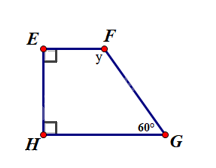
Theo định lí về tổng các góc của một tứ giác, ta có \(\widehat E + \widehat F + \widehat G + \widehat H = {360^0}\). Do đó \(\widehat F = y = {360^0} - {90^0} - {90^0} - {60^0} = {120^0}\)
Vậy \(\widehat F = {120^0}\)
Hình thang cân là một trong những hình quan trọng trong chương trình Hình học lớp 8. Việc nắm vững lý thuyết về hình thang cân là nền tảng để giải quyết các bài toán liên quan đến hình học, đặc biệt là trong các kỳ thi quan trọng.
Hình thang cân là hình thang có hai cạnh bên song song. Nói cách khác, một tứ giác là hình thang cân khi và chỉ khi nó là hình thang và hai cạnh bên bằng nhau.
Hình thang cân có những tính chất quan trọng sau:
Có những dấu hiệu sau để nhận biết một hình thang cân:
Lý thuyết hình thang cân được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là:
Để hiểu rõ hơn về lý thuyết hình thang cân, chúng ta hãy cùng xem xét một số bài tập vận dụng:
Bài tập 1: Cho hình thang cân ABCD (AB // CD). Biết góc A = 80 độ. Tính góc B, góc C, góc D.
Giải: Vì ABCD là hình thang cân nên góc A = góc B = 80 độ. Góc C = góc D = 180 độ - 80 độ = 100 độ.
Bài tập 2: Cho hình thang cân ABCD (AB // CD). Biết AC = BD = 5cm. Tính độ dài các cạnh bên AD và BC.
Giải: Vì ABCD là hình thang cân nên AD = BC. Do đó, AD = BC = 5cm.
Ngoài những kiến thức cơ bản trên, chúng ta có thể tìm hiểu thêm về các tính chất và ứng dụng nâng cao của hình thang cân, chẳng hạn như:
Hy vọng rằng bài học về Lý thuyết Hình thang cân SGK Toán 8 - Kết nối tri thức này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập liên quan.
Chúc bạn học tập tốt!