Bài 3.42 trang 74 SGK Toán 8 tập 1 thuộc chương 3: Các góc ở vị trí đặc biệt được tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.42 trang 74 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau
Đề bài
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Giả sử tứ giác ABCD có hai đường chéo bằng nhau AC = BD và AD = BC. Chứng minh ABCD là hình thang mà AC = BD nên ABCD là hình thang cân.
Lời giải chi tiết
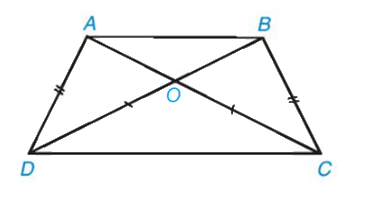
Gọi O là giao điểm của AC và BD.
Xét ∆ABC và ∆BAD có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh AB chung
Do đó ∆ABC = ∆BAD (c.c.c)
Suy ra \(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (hai góc tương ứng).
Xét ∆ACD và ∆BDC có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh CD chung
Do đó ∆ADC = ∆BCD (c.c.c)
Suy ra \(\widehat {DAC} = \widehat {CB{\rm{D}}}\) (hai góc tương ứng).
Xét ∆OAD và ∆OBC có:
\(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (chứng minh trên)
AD = BC (giả thiết)
\(\widehat {DAC} = \widehat {CB{\rm{D}}}\) (chứng minh trên)
Do đó ∆OAD = ∆OBC (g.c.g).
Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).
Khi đó, các tam giác OAB, OCD là tam giác cân tại O.
Suy ra \(\widehat {OAB} = \widehat {OBA};\widehat {OC{\rm{D}}} = \widehat {O{\rm{D}}C}\)
Xét ∆OAB và ∆OCD cân tại O có:
• \(\widehat {AOB} = \widehat {CO{\rm{D}}}\) (hai góc đối đỉnh)
• \(\widehat {OAB} = \widehat {OBA};\widehat {OC{\rm{D}}} = \widehat {O{\rm{D}}C}\)
• \(\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = \widehat {OC{\rm{D}}} + \widehat {O{\rm{D}}C} + \widehat {CO{\rm{D}}} = {180^o}\)
\(\begin{array}{l}\widehat {OAB} + \widehat {OBA} = \widehat {OC{\rm{D}}} + \widehat {O{\rm{D}}C}\\2\widehat {OAB} = 2\widehat {OC{\rm{D}}}\end{array}\)
Suy ra \(\widehat {OAB} = \widehat {OC{\rm{D}}}\) mà hai góc này ở vị trí so le trong.
Do đó AB // CD.
Tứ giác ABCD có AB // CD nên ABCD là hình thang.
Hình thang ABCD có hai đường chéo AC = BD.
Do đó tứ giác ABCD là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
Bài 3.42 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa và tính chất của các góc so le trong, đồng vị, trong cùng phía.
Cho hình vẽ sau (hình vẽ minh họa bài 3.42 SGK Toán 8 tập 1 - Kết nối tri thức). Biết a // b và ∠A1 = 40o. Tính ∠B1.
Vì a // b nên ∠A1 = ∠B1 (hai góc đồng vị).
Mà ∠A1 = 40o nên ∠B1 = 40o.
Bài giải trên dựa trên tính chất của hai đường thẳng song song và các góc đồng vị. Khi hai đường thẳng song song, các góc đồng vị bằng nhau. Do đó, để tìm ∠B1, ta chỉ cần biết giá trị của ∠A1.
Ngoài bài tập 3.42, chương 3 SGK Toán 8 tập 1 - Kết nối tri thức còn nhiều bài tập khác giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Các em học sinh nên làm đầy đủ các bài tập trong SGK và sách bài tập để nắm vững kiến thức và đạt kết quả tốt trong các bài kiểm tra.
Khi giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em học sinh nên:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập 3.42 trang 74 SGK Toán 8 tập 1 - Kết nối tri thức, các em học sinh sẽ hiểu rõ hơn về kiến thức và kỹ năng giải toán. Chúc các em học tập tốt!