Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 67, 68 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án đầy đủ và cách giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
Video hướng dẫn giải
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
Phương pháp giải:
Dựa vào định nghĩa hình thoi
Lời giải chi tiết:
Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau.
Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau:
- Hình thoi có hai góc đối bằng nhau.
- Hình thoi có các cặp cạnh đối song song.
- Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Video hướng dẫn giải
Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48).
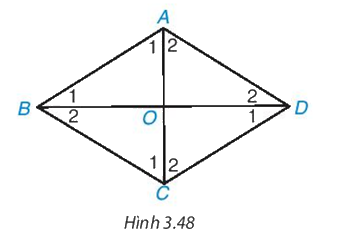
a) ∆ABD có cân tại A không?
b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao?
Phương pháp giải:
Dựa vào định nghĩa hình thoi.
Lời giải chi tiết:
a) Vì tứ giác ABCD là hình thoi nên AB = AD.
Suy ra ∆ABD có cân tại A.
b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA.
Xét ∆ABC và ∆ADC có:
AB = AD (chứng minh trên);
BC = CD (chứng minh trên);
Cạnh AC chung.
Do đó ∆ABC = ∆ADC (c.c.c)
Suy ra \(\)\(\widehat {{A_1}} = \widehat {{A_2}}\)(hai góc tương ứng)
Hay AC là đường phân giác của góc A.
Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao.
Khi đó AO ⊥ BD hay AC ⊥ BD.
Vậy AC vuông góc với BD và AC là đường phân giác của góc A.
Video hướng dẫn giải
Hãy viết giả thiết, kết luận của câu c trong Định lí 2.
Phương pháp giải:
Vẽ hình và viết giả thiết kết luận
Lời giải chi tiết:
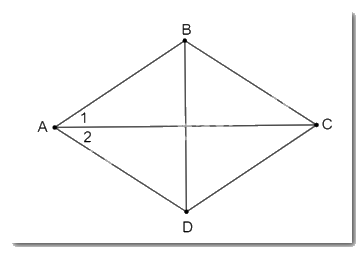
Giả thiết, kết luận của Định lí 2.
a)
GT | Hình bình hành ABCD có AB = BC. |
KL | ABCD là hình thoi. |
Ta có thể viết giả thiết đối với các cặp cạnh kề khác, chẳng hạn như:
Hình bình hành ABCD có BC = CD hoặc CD = DA hoặc DA = AB.
b)
GT | Hình bình hành ABCD có AC ⊥ BD. |
KL | ABCD là hình thoi. |
c)
GT | Hình bình hành ABCD có \(\widehat {{A_1}} = \widehat {{A_2}}\). |
KL | ABCD là hình thoi. |
Ta có thể viết giả thiết tương tự đối với tia phân giác góc B hoặc góc C hoặc góc D.
Video hướng dẫn giải
Trong Hình 3.51, hình nào là hình thoi? Vì sao?
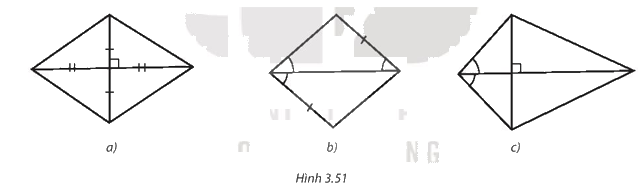
Phương pháp giải:
Quan sát hình 3.51 và dựa vào các dấu hiệu nhận biết hình thoi
Lời giải chi tiết:
• Hình 3.51a)
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
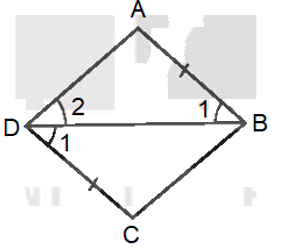
• Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD.
Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên AB // CD.
Mà AB = CD nên tứ giác ABCD là hình bình hành.
Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay DB là tia phân giác của \(\widehat {A{\rm{D}}C}\)
Khi đó, hình bình hành ABCD có DB là tia phân giác của \(\widehat {A{\rm{D}}C}\).
Do đó tứ giác ABCD là hình thoi.
• Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.
Video hướng dẫn giải
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
Phương pháp giải:
Dựa vào định nghĩa hình thoi
Lời giải chi tiết:
Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau.
Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau:
- Hình thoi có hai góc đối bằng nhau.
- Hình thoi có các cặp cạnh đối song song.
- Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Video hướng dẫn giải
Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48).
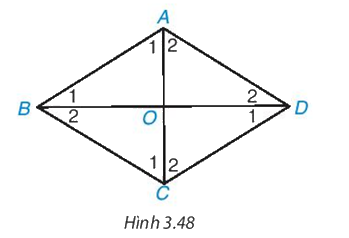
a) ∆ABD có cân tại A không?
b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao?
Phương pháp giải:
Dựa vào định nghĩa hình thoi.
Lời giải chi tiết:
a) Vì tứ giác ABCD là hình thoi nên AB = AD.
Suy ra ∆ABD có cân tại A.
b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA.
Xét ∆ABC và ∆ADC có:
AB = AD (chứng minh trên);
BC = CD (chứng minh trên);
Cạnh AC chung.
Do đó ∆ABC = ∆ADC (c.c.c)
Suy ra \(\)\(\widehat {{A_1}} = \widehat {{A_2}}\)(hai góc tương ứng)
Hay AC là đường phân giác của góc A.
Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao.
Khi đó AO ⊥ BD hay AC ⊥ BD.
Vậy AC vuông góc với BD và AC là đường phân giác của góc A.
Video hướng dẫn giải
Hãy viết giả thiết, kết luận của câu c trong Định lí 2.
Phương pháp giải:
Vẽ hình và viết giả thiết kết luận
Lời giải chi tiết:
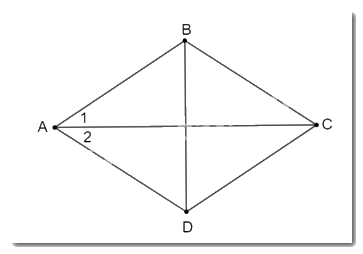
Giả thiết, kết luận của Định lí 2.
a)
GT | Hình bình hành ABCD có AB = BC. |
KL | ABCD là hình thoi. |
Ta có thể viết giả thiết đối với các cặp cạnh kề khác, chẳng hạn như:
Hình bình hành ABCD có BC = CD hoặc CD = DA hoặc DA = AB.
b)
GT | Hình bình hành ABCD có AC ⊥ BD. |
KL | ABCD là hình thoi. |
c)
GT | Hình bình hành ABCD có \(\widehat {{A_1}} = \widehat {{A_2}}\). |
KL | ABCD là hình thoi. |
Ta có thể viết giả thiết tương tự đối với tia phân giác góc B hoặc góc C hoặc góc D.
Video hướng dẫn giải
Trong Hình 3.51, hình nào là hình thoi? Vì sao?
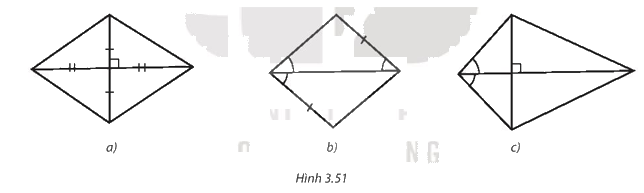
Phương pháp giải:
Quan sát hình 3.51 và dựa vào các dấu hiệu nhận biết hình thoi
Lời giải chi tiết:
• Hình 3.51a)
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
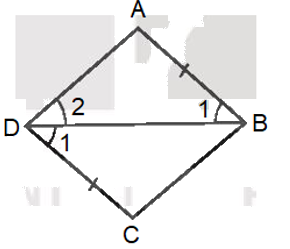
• Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD.
Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên AB // CD.
Mà AB = CD nên tứ giác ABCD là hình bình hành.
Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay DB là tia phân giác của \(\widehat {A{\rm{D}}C}\)
Khi đó, hình bình hành ABCD có DB là tia phân giác của \(\widehat {A{\rm{D}}C}\).
Do đó tứ giác ABCD là hình thoi.
• Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.
Mục 1 trang 67, 68 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép toán với đa thức. Các bài tập trong mục này yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đa thức để thực hiện các phép tính và rút gọn biểu thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 8.
Mục 1 bao gồm một số bài tập với mức độ khó tăng dần, từ việc thực hiện các phép tính đơn giản đến việc rút gọn các biểu thức phức tạp. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu ngoặc, quy tắc đổi dấu và các tính chất của phép toán.
Bài tập này yêu cầu học sinh rút gọn các biểu thức chứa đa thức. Để giải bài tập này, học sinh cần áp dụng các quy tắc về phép toán với đa thức và các tính chất của phép toán để đưa biểu thức về dạng đơn giản nhất.
Ví dụ: Rút gọn biểu thức 3x(x - 2y) + 2y(x + 3x) = ?
Bài tập này yêu cầu học sinh tìm giá trị của x thỏa mãn một phương trình chứa đa thức. Để giải bài tập này, học sinh cần áp dụng các quy tắc về giải phương trình và các phép toán với đa thức.
Ví dụ: Tìm x biết 2x + 5 = 11
Để giải các bài tập trong mục 1 trang 67, 68 SGK Toán 8 tập 1 - Kết nối tri thức một cách hiệu quả, học sinh nên:
Khi giải bài tập về đa thức, học sinh cần chú ý đến các dấu ngoặc và quy tắc đổi dấu. Việc thực hiện đúng các quy tắc này sẽ giúp tránh được các lỗi sai không đáng có.
Mục 1 trang 67, 68 SGK Toán 8 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán 8. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này sẽ giúp học sinh tự tin hơn khi đối mặt với các bài toán khó hơn trong tương lai. giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho các em những thông tin hữu ích và giúp các em học tốt môn Toán 8.
| Bài tập | Nội dung | Mức độ khó |
|---|---|---|
| Bài 1 | Thực hiện các phép tính với đa thức | Dễ |
| Bài 2 | Rút gọn biểu thức chứa đa thức | Trung bình |
| Bài 3 | Tìm x trong phương trình chứa đa thức | Trung bình - Khó |