Bài 4 trang 114 SGK Toán 8 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học về hình hộp chữ nhật và hình lập phương. Bài tập này thường yêu cầu tính toán diện tích xung quanh, diện tích toàn phần và thể tích của các hình này.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 114 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm thương và dư (nếu có) trong các phép chia sau:
Đề bài
Tìm thương và dư (nếu có) trong các phép chia sau:
\(\begin{array}{l}a)\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\\b)\left( {2{{\rm{x}}^3} + 5{{\rm{x}}^2} - 2{\rm{x}} + 12} \right):\left( {2{{\rm{x}}^2} - x + 1} \right)\end{array}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
Lời giải chi tiết
a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\)
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
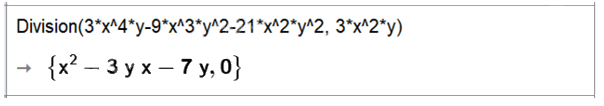
Vậy phép chia hai đa thức \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right)\) cho \(3{{\rm{x}}^2}y\), ta được thương là \({x^2} - 3{\rm{x}}y - 7y\) và dư 0.
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
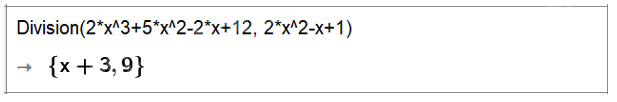
Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.
Bài 4 trang 114 SGK Toán 8 tập 1 - Kết nối tri thức là một bài toán thực tế, yêu cầu học sinh vận dụng kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hai hình này.
Trong đó:
(Nội dung bài giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, công thức sử dụng, và kết quả cuối cùng. Bài giải sẽ được phân tích rõ ràng, dễ hiểu để học sinh có thể tự học và áp dụng vào các bài tập tương tự.)
Ví dụ, nếu bài toán yêu cầu tính diện tích xung quanh của một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm, ta sẽ áp dụng công thức:
Diện tích xung quanh = 2(5 + 3) * 4 = 64 cm2
Ngoài bài 4 trang 114, SGK Toán 8 tập 1 - Kết nối tri thức còn có nhiều bài tập tương tự khác. Để giải quyết các bài tập này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hình hộp chữ nhật và hình lập phương, học sinh có thể luyện tập thêm các bài tập sau:
Bài 4 trang 114 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình hộp chữ nhật và hình lập phương. Bằng cách nắm vững lý thuyết, áp dụng đúng công thức và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| Diện tích xung quanh hình hộp chữ nhật | 2(a + b)h |
| Diện tích toàn phần hình hộp chữ nhật | 2(ab + ah + bh) |
| Thể tích hình hộp chữ nhật | abh |