Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 95, 96, 97 sách giáo khoa Toán 8 tập 2 chương trình Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, logic và giúp các em nắm vững kiến thức.
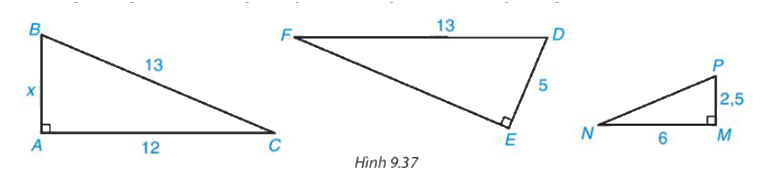
Cho tam giác vuông với kích thước như Hình 9.37
Video hướng dẫn giải
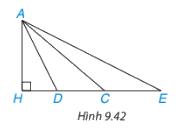
Cho hình 9.42, trong đó các đoạn thẳng AC, AD, AE đoạn nào có độ dài lớn nhất, đoạn nào có độ dài nhỏ nhất?
Phương pháp giải:
Áp dụng định lí Pythagore trong các tam giác vuông.
Lời giải chi tiết:
Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có: \(A{{\rm{D}}^2} = A{H^2} + H{{\rm{D}}^2}\) (1)
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có: \(A{C^2} = A{H^2} + H{C^2}\) (2)
Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có: \(A{E^2} = A{H^2} + H{E^2}\) (3)
Vì HE > HC > HD suy ra \(H{E^2} > H{C^2} > H{{\rm{D}}^2}\)(4)
Từ (1), (2), (3), (4) suy ra: \(A{{\rm{E}}^2} > A{C^2} > A{{\rm{D}}^2} \Rightarrow A{\rm{E}} > AC > A{\rm{D}}\)
Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.
Video hướng dẫn giải
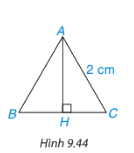
Tính chiều cao theo đơn vị centimét của một tam giác đều cạnh 2cm (h.9.44) (làm tròn kết quả đến chữ số thập phân thứ hai)
Phương pháp giải:
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC.
Áp đụng định lí Pythagore trong tam giác AHC suy ra độ dài của chiều cao
Lời giải chi tiết:
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1, 73 cm
Video hướng dẫn giải
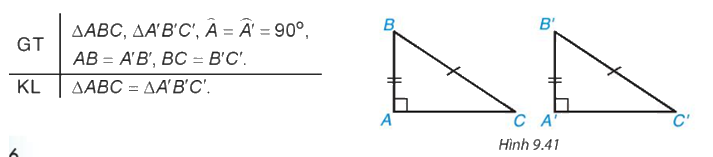
Trước đây chúng ta thừa nhận định lí về trường hợp bằng nhau đặc biệt của hai tam giác vuông: "Nếu một cạnh góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó bằng nhau”.
Phương pháp giải:
Áp dụng định lí Pythagore trong hai tam giác vuông để suy ra cặp cạnh bằng nhau
Lời giải chi tiết:
- Xét tam giác ABC vuông tại A, có
\(\)\(B{C^2} = A{B^2} + A{C^2}\)(1)
- Xét tam giác A'B'C' vuông tại A' có:
\(B'C{'^2} = A'B{'^2} + A'C{'^2}\) (2)
mà AB=A’B’, BC=B’C’ (3)
=> Từ (1), (2), (3): AC= A’C’
=> Hai tam giác bằng nhau
Video hướng dẫn giải
Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông ABC vuông tại A để tính x
Lời giải chi tiết:
Áp dụng định lí Pythagore vào \(\Delta ABC\) ta có:
\(x = AB = \sqrt{13^2-12^2} = 5\)
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1 \( \left( \frac{AB}{DE} = \frac{BC}{DF} = 1 \right) \)
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\) \( \left( \frac{MP}{AB} = \frac{MN}{AC} = \frac{2,5}{5} = \frac{6}{12} = \frac{1}{2} \right) \)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\) (do tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\) và tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1 nên tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2} . 1 = \frac{1}{2}\) )
Video hướng dẫn giải
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3km đến điểm B thì rẽ vuông góc sang trái, chạy được 3km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khác là bao nhiêu kilômét.
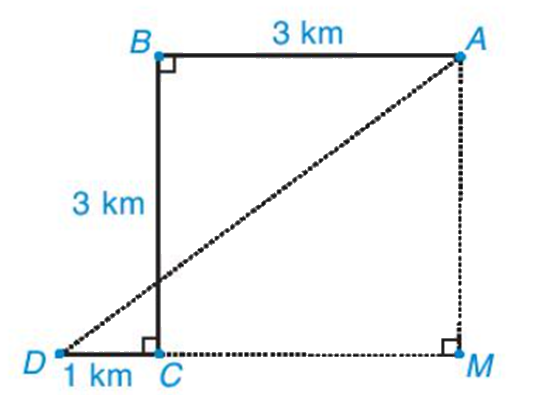
Phương pháp giải:
Áp dụng định lí Pythagore trong tam giác AMD vuông tại M
Lời giải chi tiết:
Ta có: BC=AM=3km
AB=CM=3km
=> MD=CM+CD=3+1=4(km)
Xét tam giác AMD vuông tại M
=> \(A{{\rm{D}}^2} = A{M^2} + M{{\rm{D}}^2}\)
=> \(A{{\rm{D}}^2} = {3^2} + {4^2}\)
=> AD=5
Vậy lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là 5km
Video hướng dẫn giải
Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng
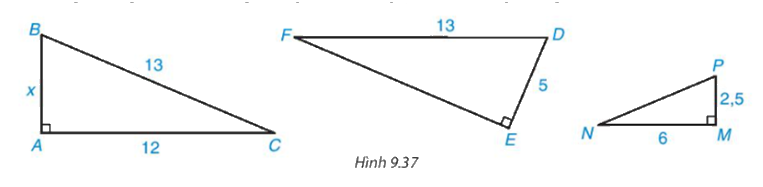
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông ABC vuông tại A để tính x
Lời giải chi tiết:
Áp dụng định lí Pythagore vào \(\Delta ABC\) ta có:
\(x = AB = \sqrt{13^2-12^2} = 5\)
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1 \( \left( \frac{AB}{DE} = \frac{BC}{DF} = 1 \right) \)
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\) \( \left( \frac{MP}{AB} = \frac{MN}{AC} = \frac{2,5}{5} = \frac{6}{12} = \frac{1}{2} \right) \)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\) (do tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\) và tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1 nên tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2} . 1 = \frac{1}{2}\) )
Video hướng dẫn giải
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3km đến điểm B thì rẽ vuông góc sang trái, chạy được 3km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khác là bao nhiêu kilômét.
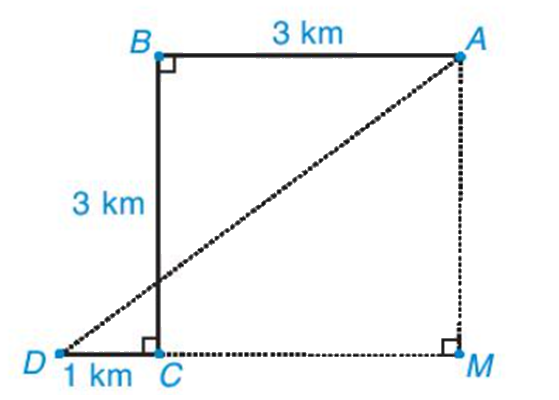
Phương pháp giải:
Áp dụng định lí Pythagore trong tam giác AMD vuông tại M
Lời giải chi tiết:
Ta có: BC=AM=3km
AB=CM=3km
=> MD=CM+CD=3+1=4(km)
Xét tam giác AMD vuông tại M
=> \(A{{\rm{D}}^2} = A{M^2} + M{{\rm{D}}^2}\)
=> \(A{{\rm{D}}^2} = {3^2} + {4^2}\)
=> AD=5
Vậy lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là 5km
Video hướng dẫn giải
Cho hình 9.42, trong đó các đoạn thẳng AC, AD, AE đoạn nào có độ dài lớn nhất, đoạn nào có độ dài nhỏ nhất?
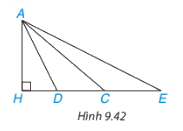
Phương pháp giải:
Áp dụng định lí Pythagore trong các tam giác vuông.
Lời giải chi tiết:
Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có: \(A{{\rm{D}}^2} = A{H^2} + H{{\rm{D}}^2}\) (1)
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có: \(A{C^2} = A{H^2} + H{C^2}\) (2)
Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có: \(A{E^2} = A{H^2} + H{E^2}\) (3)
Vì HE > HC > HD suy ra \(H{E^2} > H{C^2} > H{{\rm{D}}^2}\)(4)
Từ (1), (2), (3), (4) suy ra: \(A{{\rm{E}}^2} > A{C^2} > A{{\rm{D}}^2} \Rightarrow A{\rm{E}} > AC > A{\rm{D}}\)
Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.
Video hướng dẫn giải
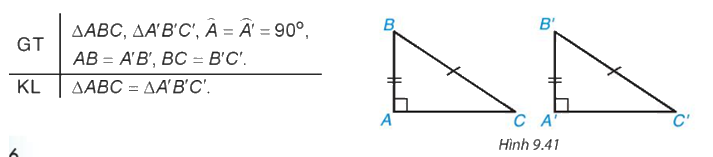
Trước đây chúng ta thừa nhận định lí về trường hợp bằng nhau đặc biệt của hai tam giác vuông: "Nếu một cạnh góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó bằng nhau”.
Phương pháp giải:
Áp dụng định lí Pythagore trong hai tam giác vuông để suy ra cặp cạnh bằng nhau
Lời giải chi tiết:
- Xét tam giác ABC vuông tại A, có
\(\)\(B{C^2} = A{B^2} + A{C^2}\)(1)
- Xét tam giác A'B'C' vuông tại A' có:
\(B'C{'^2} = A'B{'^2} + A'C{'^2}\) (2)
mà AB=A’B’, BC=B’C’ (3)
=> Từ (1), (2), (3): AC= A’C’
=> Hai tam giác bằng nhau
Video hướng dẫn giải
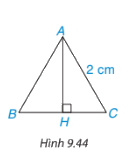
Tính chiều cao theo đơn vị centimét của một tam giác đều cạnh 2cm (h.9.44) (làm tròn kết quả đến chữ số thập phân thứ hai)
Phương pháp giải:
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC.
Áp đụng định lí Pythagore trong tam giác AHC suy ra độ dài của chiều cao
Lời giải chi tiết:
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1, 73 cm
Mục 2 của chương trình Toán 8 tập 2 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài tập phức tạp hơn trong các chương tiếp theo.
Bài tập này yêu cầu học sinh vận dụng các tính chất của hình bình hành để chứng minh các tính chất khác, giải các bài toán liên quan đến diện tích và chu vi của hình bình hành. Các em cần nhớ rõ các định nghĩa, định lý và tính chất cơ bản của hình bình hành để giải quyết bài tập một cách hiệu quả.
Hình chữ nhật là một trường hợp đặc biệt của hình bình hành, có thêm tính chất các góc vuông. Bài tập trong phần này thường yêu cầu học sinh chứng minh một tứ giác là hình chữ nhật, tính toán diện tích và chu vi của hình chữ nhật, và giải các bài toán ứng dụng thực tế.
Hình thoi là một hình bình hành đặc biệt có các cạnh bằng nhau. Bài tập về hình thoi thường tập trung vào việc chứng minh một tứ giác là hình thoi, tính toán diện tích của hình thoi, và giải các bài toán liên quan đến đường chéo của hình thoi.
Hình vuông là một hình chữ nhật đặc biệt có các cạnh bằng nhau. Bài tập về hình vuông thường yêu cầu học sinh chứng minh một tứ giác là hình vuông, tính toán diện tích và chu vi của hình vuông, và giải các bài toán ứng dụng thực tế.
Bài tập: Cho hình bình hành ABCD, có góc A bằng 60 độ. Tính các góc còn lại của hình bình hành.
Giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 8 tập 2 hoặc trên các trang web học toán online khác.
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập lý thuyết, làm bài tập và tìm hiểu các phương pháp giải bài tập hiệu quả. Chúc các em học tốt!
| Hình | Tính chất |
|---|---|
| Hình bình hành | Các cạnh đối song song và bằng nhau, các góc đối bằng nhau. |
| Hình chữ nhật | Có bốn góc vuông. |
| Hình thoi | Có bốn cạnh bằng nhau. |
| Hình vuông | Có bốn cạnh bằng nhau và bốn góc vuông. |