Bài 5.7 trang 98 SGK Toán 8 tập 1 thuộc chương 3: Các góc ở vị trí đặc biệt được tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.7 trang 98 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 8.
Bảng sau cho biết khối lượng giấy vụn các lớp khối 8 đã thu gom được. Lựa chọn biểu đồ phù hợp biểu diễn bảng thống kê này. Vẽ biểu đồ đó.
Đề bài
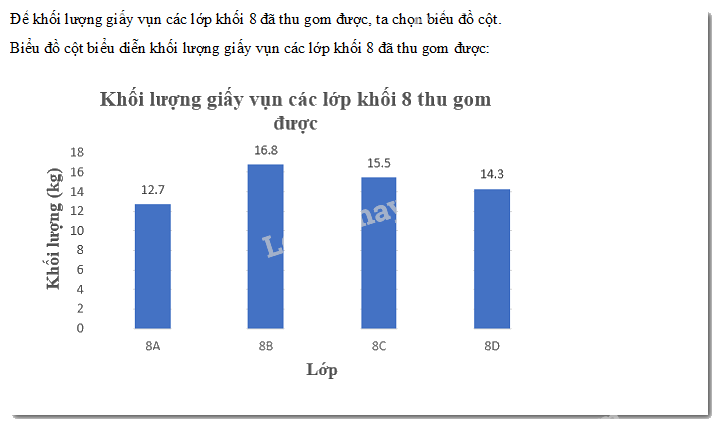
Bảng sau cho biết khối lượng giấy vụn các lớp khối 8 đã thu gom được.

Lựa chọn biểu đồ phù hợp biểu diễn bảng thống kê này. Vẽ biểu đồ đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Vẽ biểu đồ cột
Lời giải chi tiết
Bài 5.7 trang 98 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương 3, giúp học sinh củng cố kiến thức về các góc ở vị trí đặc biệt được tạo bởi một đường thẳng cắt hai đường thẳng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và tính chất sau:
Đề bài: Cho hình vẽ, biết a // b và ∠A1 = 40o. Tính ∠B1.
Lời giải:
Vì a // b nên ∠A1 = ∠B1 (hai góc đồng vị).
Mà ∠A1 = 40o nên ∠B1 = 40o.
Kết luận: ∠B1 = 40o.
Để giải bài tập 5.7 trang 98 SGK Toán 8 tập 1 - Kết nối tri thức, học sinh cần:
Để hiểu rõ hơn về cách giải các bài tập về góc ở vị trí đặc biệt, chúng ta cùng xem xét một số ví dụ sau:
Ví dụ 1: Cho hình vẽ, biết a // b và ∠A2 = 60o. Tính ∠B2.
Lời giải: Vì a // b nên ∠A2 = ∠B2 (hai góc so le trong). Mà ∠A2 = 60o nên ∠B2 = 60o.
Ví dụ 2: Cho hình vẽ, biết a // b và ∠A3 + ∠B3 = 180o. Chứng minh rằng a // b.
Lời giải: Vì ∠A3 + ∠B3 = 180o (hai góc trong cùng phía) nên a // b (dấu hiệu nhận biết hai đường thẳng song song).
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về góc ở vị trí đặc biệt, học sinh có thể tự giải thêm các bài tập sau:
Bài 5.7 trang 98 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các góc ở vị trí đặc biệt và các tính chất của chúng. Bằng cách nắm vững kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tự tin giải quyết các bài toán tương tự trong các kỳ thi và bài kiểm tra.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và dễ hiểu này sẽ giúp các em học sinh học tập tốt môn Toán 8. Chúc các em học tập tốt!