Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 93, 94, 95 sách giáo khoa Toán 8 tập 2 - Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp cho các em những phương pháp giải bài tập hiệu quả nhất, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Cho tam giác vuông ABC có hai cạnh góc vuông
Video hướng dẫn giải
Cho tam giác vuông ABC có hai cạnh góc vuông AB=3cm,AC=4cm (H.9.31). Hãy đo độ dài cạnh BC và so sánh hai đại lượng \(A{B^2} + A{C^2}\) với \(B{C^2}\)
Phương pháp giải:
Thay các giá trị AB=3cm, AC=4cm vào \(A{B^2} + A{C^2}\) với \(B{C^2}\)
Lời giải chi tiết:
- Đo độ dài có BC=5cm
- Có \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
với \(B{C^2} = {5^2} = 25\)
=>\(A{B^2} + A{C^2} = B{C^2}\)
Video hướng dẫn giải
Em hãy giải bài toán mở đầu:
Bạn Lan vẽ một hình chữ nhật với chiều rộng và chiều dài lần lượt là 1; 3 (đơn vị độ dài). Sau đó Lan đặt lên trục số đoạn OM có độ dài bằng độ dài của đường chéo hình chữ nhật vừa vẽ (trục số nằm ngang và M nằm bên phải gốc O). Hỏi điểm M biểu diễn số thực nào? Biết rằng đơn vị độ dài trên trục số và đơn vị độ dài đo kích thước hình chữ nhật là như nhau.
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông ABC vuông tại A
Lời giải chi tiết:
- Nếu điểm M biểu diễn cho số thực x thì đoạn thẳng OM có độ dài là x (đvđd).– Đoạn thẳng OM là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là hai cạnh của hình chữ nhật. Do đó, áp dụng định lý Pythagore cho tam giác này, ta được: \( x^2 =1^2+3^2 =10\). Suy ra x=\( \sqrt {10}\).
Video hướng dẫn giải
Tìm độ dài x, y trong hình 9.35
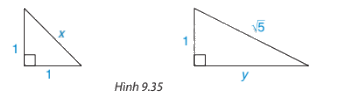
Phương pháp giải:
Áp dụng định lý Pythagore
Lời giải chi tiết:
Ta có: \({x^2} = {1^2} + {1^2} = 2 \Rightarrow x = \sqrt 2 \)
Ta có: \({\left( {\sqrt 5 } \right)^2} = {1^2} + {y^2} \Rightarrow {y^2} = {\left( {\sqrt 5 } \right)^2} - {1^2} = 5 - 1 = 4 \Rightarrow y = 2\)
Video hướng dẫn giải
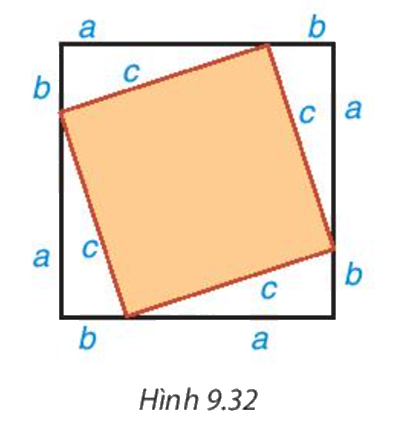
Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32
- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c
- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?
- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao nhiêu?
- So sánh \({c^2} + 2{\rm{a}}b\) với \({\left( {a + b} \right)^2}\)để rút ra nhận xét về mối quan hệ giữa hai đại lượng \({c^2}\) và \({a^2} + {b^2}\).
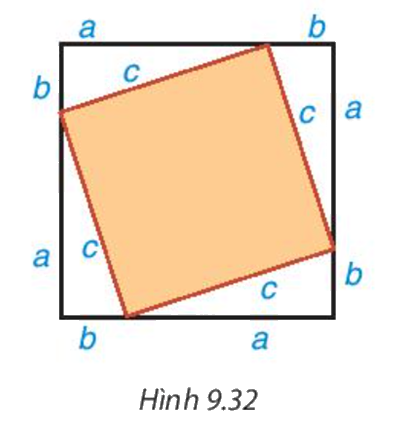
Phương pháp giải:
- Tính diện tích tấm bìa của hình vuông.
- Tính diện tích phần bìa bị che lấp là hình vuông cạnh c.
Lời giải chi tiết:
Phần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là: \({c^2}\)
- Diện tích tấm bìa hình vuông là: \({\left( {a + b} \right)^2}\)
=> Diện tích bốn tam giác vuông là: \({\left( {a + b} \right)^2} - {c^2}\)
Video hướng dẫn giải
Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.
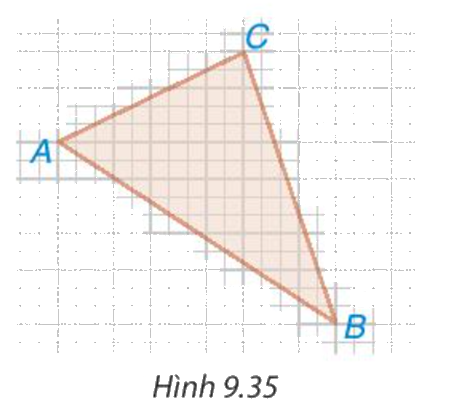
Phương pháp giải:
Áp dụng định lý Pythagore
Lời giải chi tiết:
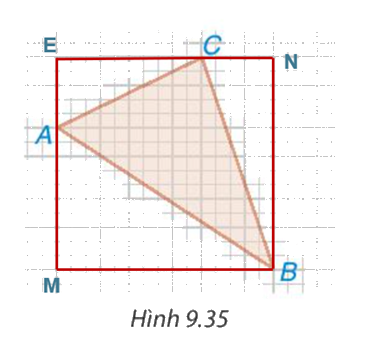
Từ A kẻ AM sao cho AM ⊥ MB
Tử C kẻ CM sao cho CN ⊥ NB
Từ C kẻ EC sao cho EC ⊥ EA
- Xét ΔAMB có AM ⊥ MB
=> ΔAMB là tam giác vuông
=> \(A{B^2} = A{M^2} + M{B^2}\)
=> \(A{B^2} = {10^2} + {15^2}\)
=> \(AB = 5\sqrt {13} \) cm
- Xét ΔBNC có CN ⊥ NB
=> ΔBNC là tam giác vuông tại N
=> \(B{C^2} = N{B^2} + N{C^2}\)
=> \(BC = {15^2} + {5^2}\)
=> \(BC = 5\sqrt {10} \)cm
- Xét ΔAEC có EC ⊥ EA
=> ΔAEC là tam giác vuông tại E
=> \(A{C^2} = E{{\rm{A}}^2} + E{C^2}\)
=> \(A{C^2} = {5^2} + {10^2}\)
=> \(AC = 5\sqrt 5 \)cm
Video hướng dẫn giải
Cho tam giác vuông ABC có hai cạnh góc vuông AB=3cm,AC=4cm (H.9.31). Hãy đo độ dài cạnh BC và so sánh hai đại lượng \(A{B^2} + A{C^2}\) với \(B{C^2}\)
Phương pháp giải:
Thay các giá trị AB=3cm, AC=4cm vào \(A{B^2} + A{C^2}\) với \(B{C^2}\)
Lời giải chi tiết:
- Đo độ dài có BC=5cm
- Có \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
với \(B{C^2} = {5^2} = 25\)
=>\(A{B^2} + A{C^2} = B{C^2}\)
Video hướng dẫn giải
Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32
- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c
- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?
- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao nhiêu?
- So sánh \({c^2} + 2{\rm{a}}b\) với \({\left( {a + b} \right)^2}\)để rút ra nhận xét về mối quan hệ giữa hai đại lượng \({c^2}\) và \({a^2} + {b^2}\).
Phương pháp giải:
- Tính diện tích tấm bìa của hình vuông.
- Tính diện tích phần bìa bị che lấp là hình vuông cạnh c.
Lời giải chi tiết:
Phần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là: \({c^2}\)
- Diện tích tấm bìa hình vuông là: \({\left( {a + b} \right)^2}\)
=> Diện tích bốn tam giác vuông là: \({\left( {a + b} \right)^2} - {c^2}\)
Video hướng dẫn giải
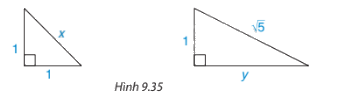
Tìm độ dài x, y trong hình 9.35
Phương pháp giải:
Áp dụng định lý Pythagore
Lời giải chi tiết:
Ta có: \({x^2} = {1^2} + {1^2} = 2 \Rightarrow x = \sqrt 2 \)
Ta có: \({\left( {\sqrt 5 } \right)^2} = {1^2} + {y^2} \Rightarrow {y^2} = {\left( {\sqrt 5 } \right)^2} - {1^2} = 5 - 1 = 4 \Rightarrow y = 2\)
Video hướng dẫn giải
Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.
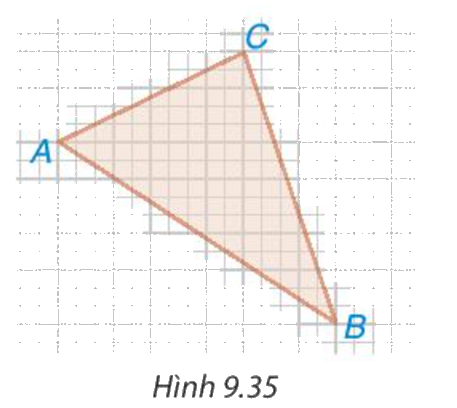
Phương pháp giải:
Áp dụng định lý Pythagore
Lời giải chi tiết:
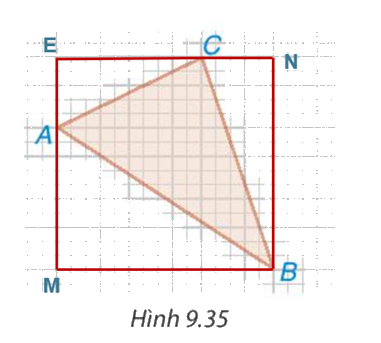
Từ A kẻ AM sao cho AM ⊥ MB
Tử C kẻ CM sao cho CN ⊥ NB
Từ C kẻ EC sao cho EC ⊥ EA
- Xét ΔAMB có AM ⊥ MB
=> ΔAMB là tam giác vuông
=> \(A{B^2} = A{M^2} + M{B^2}\)
=> \(A{B^2} = {10^2} + {15^2}\)
=> \(AB = 5\sqrt {13} \) cm
- Xét ΔBNC có CN ⊥ NB
=> ΔBNC là tam giác vuông tại N
=> \(B{C^2} = N{B^2} + N{C^2}\)
=> \(BC = {15^2} + {5^2}\)
=> \(BC = 5\sqrt {10} \)cm
- Xét ΔAEC có EC ⊥ EA
=> ΔAEC là tam giác vuông tại E
=> \(A{C^2} = E{{\rm{A}}^2} + E{C^2}\)
=> \(A{C^2} = {5^2} + {10^2}\)
=> \(AC = 5\sqrt 5 \)cm
Video hướng dẫn giải
Em hãy giải bài toán mở đầu:
Bạn Lan vẽ một hình chữ nhật với chiều rộng và chiều dài lần lượt là 1; 3 (đơn vị độ dài). Sau đó Lan đặt lên trục số đoạn OM có độ dài bằng độ dài của đường chéo hình chữ nhật vừa vẽ (trục số nằm ngang và M nằm bên phải gốc O). Hỏi điểm M biểu diễn số thực nào? Biết rằng đơn vị độ dài trên trục số và đơn vị độ dài đo kích thước hình chữ nhật là như nhau.
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông ABC vuông tại A
Lời giải chi tiết:
- Nếu điểm M biểu diễn cho số thực x thì đoạn thẳng OM có độ dài là x (đvđd).– Đoạn thẳng OM là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là hai cạnh của hình chữ nhật. Do đó, áp dụng định lý Pythagore cho tam giác này, ta được: \( x^2 =1^2+3^2 =10\). Suy ra x=\( \sqrt {10}\).
Mục 1 của chương trình Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa các kiến thức về tứ giác. Các bài tập trong trang 93, 94, 95 SGK Toán 8 tập 2 yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế liên quan đến tứ giác, đặc biệt là hình thang cân.
Bài 1 yêu cầu học sinh nhắc lại các định nghĩa, tính chất của các loại tứ giác đã học (hình bình hành, hình chữ nhật, hình thoi, hình vuông, hình thang cân). Đồng thời, học sinh cần biết cách chứng minh một tứ giác là một loại tứ giác cụ thể dựa trên các điều kiện cho trước.
Bài 2 tập trung vào việc vận dụng các tính chất của hình thang cân để giải các bài toán liên quan đến góc, cạnh, đường chéo. Học sinh cần nắm vững các tính chất như: hai góc kề một đáy bằng nhau, hai đường chéo bằng nhau, tổng hai góc kề một cạnh bên bằng 180 độ.
Ví dụ: Cho hình thang cân ABCD (AB // CD). Biết góc A = 80 độ. Tính góc B, góc C, góc D.
Giải: Vì ABCD là hình thang cân nên góc B = góc A = 80 độ. Góc C = góc D. Mà tổng bốn góc trong một tứ giác bằng 360 độ nên góc C = góc D = (360 - 80 - 80) / 2 = 100 độ.
Bài 3 đưa ra các bài toán thực tế liên quan đến hình thang cân, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết. Các bài toán này thường liên quan đến việc tính độ dài các cạnh, đường cao, diện tích của hình thang cân.
Ví dụ: Một mảnh đất hình thang cân có đáy lớn 20m, đáy nhỏ 10m, chiều cao 8m. Tính diện tích mảnh đất đó.
Giải: Diện tích mảnh đất là: (20 + 10) * 8 / 2 = 120 (m2).
Để học tốt môn Toán 8, các em cần:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 8. Chúc các em học tốt!