Định lí Thalès là một trong những kiến thức quan trọng bậc nhất trong chương trình Toán 8, đặc biệt là chương trình Kết nối tri thức. Nắm vững định lí này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức hình học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp lý thuyết Định lí Thalès trong tam giác một cách chi tiết, dễ hiểu, kèm theo các ví dụ minh họa và bài tập vận dụng đa dạng.
Tỉ số của hai đoạn thẳng là gì?
1. Khái niệm tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
2. Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\)
3. Định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.
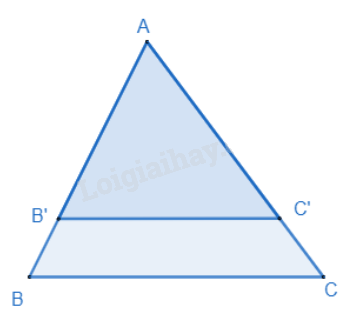
\(\Delta ABC,B'C'//BC(B' \in AB,C' \in AC) \) thì \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}};\frac{{AB'}}{{BB'}} = \frac{{AC'}}{{CC'}};\frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\)
4. Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
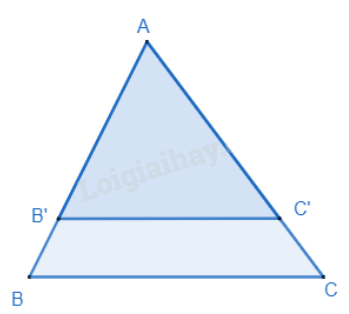
\(\Delta ABC, B' \in AB,C' \in AC, \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \) thì \(B’C’ // BC \)
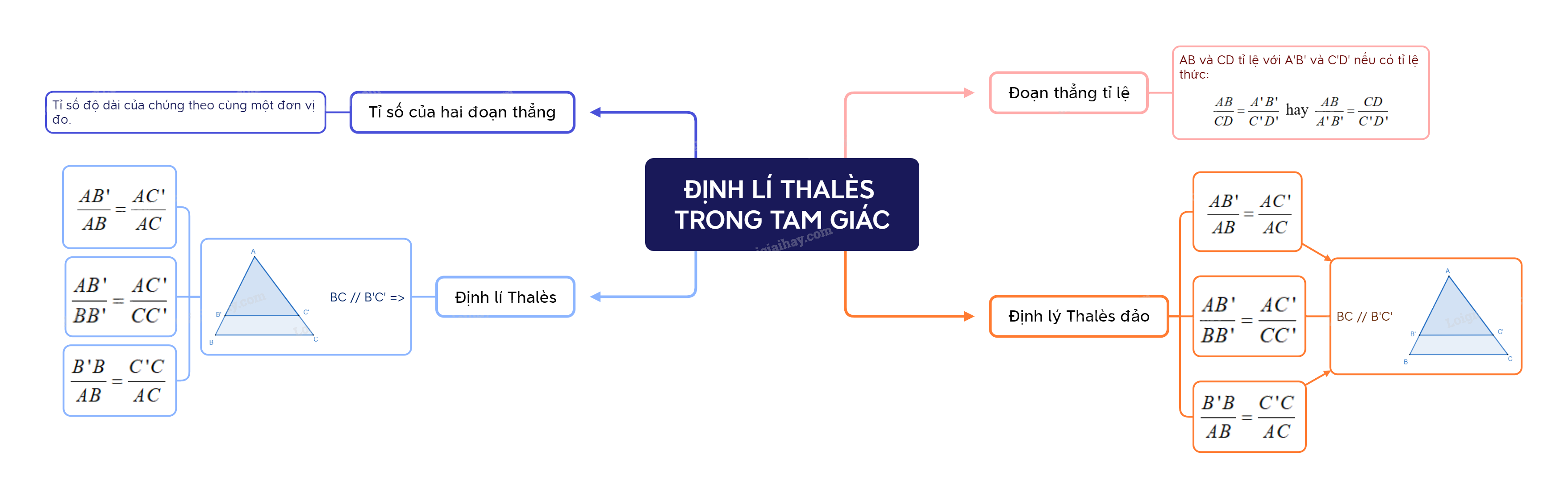
Định lí Thalès là một trong những định lý cơ bản và quan trọng trong hình học, được học trong chương trình Toán 8 Kết nối tri thức. Định lý này cung cấp một công cụ mạnh mẽ để giải quyết các bài toán liên quan đến tỉ lệ thức và các đoạn thẳng song song trong tam giác.
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó chia hai cạnh đó thành những đoạn thẳng tỉ lệ.
Cụ thể, cho tam giác ABC, đường thẳng d song song với BC cắt AB tại M và AC tại N. Khi đó:
Từ Định lí Thalès, ta có thể suy ra một số hệ quả quan trọng:
Chứng minh Định lí Thalès dựa trên việc sử dụng các tam giác đồng dạng. Cụ thể, ta xét hai tam giác AMN và ABC. Vì MN song song với BC nên:
Do đó, tam giác AMN đồng dạng với tam giác ABC (theo trường hợp góc - góc - góc). Từ đó suy ra tỉ lệ:
Biến đổi tỉ lệ trên, ta được:
Định lí Thalès có rất nhiều ứng dụng trong việc giải toán hình học, đặc biệt là:
Bài tập 1: Cho tam giác ABC, M là một điểm trên AB, N là một điểm trên AC sao cho MN song song với BC. Biết AM = 4cm, MB = 6cm, AN = 5cm. Tính độ dài NC.
Giải:
Vì MN song song với BC nên theo Định lí Thalès, ta có:
Bài tập 2: Cho tam giác ABC, MN song song với BC. Biết AM/AB = 2/5. Tính tỉ số MN/BC.
Giải:
Vì MN song song với BC nên theo hệ quả của Định lí Thalès, ta có:
Hy vọng với những kiến thức và ví dụ trên, bạn đã nắm vững lý thuyết Định lí Thalès trong tam giác SGK Toán 8 - Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.