Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 Kết nối tri thức. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương này tập trung vào các kiến thức quan trọng về hình học, đặc biệt là các định lý và tính chất liên quan đến tứ giác. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng vững chắc cho các bài học tiếp theo.
Phân tích tử và mẫu của phân thức
Video hướng dẫn giải
Phân tích tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) thành nhân tử và tìm các nhân tử chung của chúng
Phương pháp giải:
Thực hiện phân tích cả tử và mẫu của phân thức theo phân tích đa thức thành nhân tử
Lời giải chi tiết:
Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
Nhân tử chung là x + 1
Video hướng dẫn giải
Chia cả tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn
Phương pháp giải:
Thực hiện rút gọn phân thức
Lời giải chi tiết:
Ta có:\(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{2{\rm{x}}}}{{x + 1}}\)
Video hướng dẫn giải
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Phương pháp giải:
Dựa vào tính chất cơ bàn của phân thức
Lời giải chi tiết:
Ta có: \(\frac{{x - y}}{{{x^3} - {y^3}}} = \frac{{x - y}}{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{1}{{{x^2} + xy + {y^2}}}\)
Video hướng dẫn giải
Tìm a sao cho hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\)
Phương pháp giải:
Áp dụng quy tắc rút gọn phân thức
Lời giải chi tiết:
Ta có: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}} = \frac{{ - a\left( {{x^2} + x} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{ - ax\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{{\rm{ - ax}}}}{{x - 1}}\)
Để hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\) khi và chỉ khi a = -3
Video hướng dẫn giải
Cho hai phân thức: \(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}}\)và \(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}}\). Phân tích các mẫu thức của hai phân thức đã cho thành nhân tử
Phương pháp giải:
Phân tích mẫu thức của mỗi phân thức theo phân tích đa thức thành nhân tử
Lời giải chi tiết:
Ta có: \(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}} = \frac{1}{{2{\rm{x}}\left( {x + 1} \right)}}\)
\(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}} = \frac{1}{{3{\rm{x}}\left( {x - 2} \right)}}\)
Video hướng dẫn giải
Chọn mẫu thức chung (MTC) của hai mẫu thức trên bàng cách lấy tích của các nhân tử được chọn như sau:
- Nhân tử bằng số của MTC là tích các nhân tử bằng số ở các mẫu thức của các phân thức đã cho (nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử bằng số ở MTC là BCNN của chúng);
- Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa với số mũ cao nhất.
Phương pháp giải:
Thực hiện theo yêu cầu của đề bài
Lời giải chi tiết:
Mẫu thức chung: 6x(x+1)(x−2)
Video hướng dẫn giải
Tìm nhân tử phụ của mỗi mẫu thức bằng cách lấy MTC chia cho mẫu thức đó
Phương pháp giải:
Lấy MTC chia cho mẫu của mỗi phân thức
Lời giải chi tiết:
Nhân tử phụ của 2x2 +2x là 3(x−2)
Nhân tử phụ của 3x2 −6x là 2(x+1)
Video hướng dẫn giải
Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng, ta được các phân thức có mẫu thức là MTC đã chọn
Phương pháp giải:
Thực hiện theo yêu cầu của đề bài
Lời giải chi tiết:
Ta có:\(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}} = \frac{1}{{2{\rm{x}}\left( {x + 1} \right)}} = \frac{{3{\rm{x}}\left( {x - 2} \right)}}{{6{\rm{x}}\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}} = \frac{1}{{3{\rm{x}}\left( {x - 2} \right)}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{6{\rm{x}}\left( {x + 1} \right)\left( {x - 2} \right)}}\)
Video hướng dẫn giải
Quy đồng mẫu thức hai phân thức \(\frac{1}{{3{{\rm{x}}^2} - 3}}\) và \(\frac{1}{{{x^3} - 1}}\)
Phương pháp giải:
- Phân tích mẫu của hai phân thức đã cho
- Tìm MTC
- Tìm nhân tử phụ của mỗi mẫu thức
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ
Lời giải chi tiết:
Ta có:3x2 −3=3(x2−1)=3(x−1)(x+1)
x3 −1=(x−1)(x2 + x + 1)
MTC= 3(x−1)(x+1)(x2 + x + 1)
Nhân tử phụ của 3x2 − 3 là x2 + x + 1
Nhân tử phụ của x3 − 1 là 3(x+1)
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có:
\(\frac{1}{{3{{\rm{x}}^2} - 3}} = \frac{{{x^2} + x + 1}}{{3\left( {{x^2} - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{{x^2} + x + 1}}{{3\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\(\frac{1}{{{x^3} - 1}} = \frac{{3\left( {x + 1} \right)}}{{3\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)}}\)
Video hướng dẫn giải
Tròn: hai phân thức \(\frac{5}{{x - 1}}\) và \(\frac{x}{{1 - x}}\) có MTC là x – 1
Vuông: Không đúng, MTC là (x – 1)(1 – x)
Theo em, bạn nào chọn MTC hợp lí hơn? Vì sao?
Phương pháp giải:
Nhân cả tử và mẫu của phân thức \(\frac{5}{{x - 1}}\) với -1
Lời giải chi tiết:
Ta có: \(\frac{x}{{1 - x}} = \frac{{ - x}}{{x - 1}}\)
Hai phân thức \(\frac{5}{{x - 1}}\) và \(\frac{x}{{1 - x}}\) có MTC là x – 1
Bạn Tròn chọn MTC hợp lí hơn.
Video hướng dẫn giải
Thực hiện rút gọn một phân thức như hình bên . Hỏi bạn tròn làm đúng hay sai/ Vì sao?
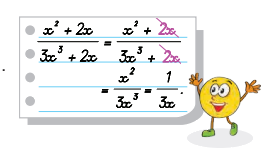
Phương pháp giải:
Dựa vào cách rút gọn một phân thức
Lời giải chi tiết:
Bạn tròn làm thế là sai. Vì bạn bỏ hai số hạng giống nhau của cả tử và mẫu là 2x chứ không phải chia cho nhân tử chung của cả tử và mẫu.
Video hướng dẫn giải
Phân tích tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) thành nhân tử và tìm các nhân tử chung của chúng
Phương pháp giải:
Thực hiện phân tích cả tử và mẫu của phân thức theo phân tích đa thức thành nhân tử
Lời giải chi tiết:
Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
Nhân tử chung là x + 1
Video hướng dẫn giải
Chia cả tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn
Phương pháp giải:
Thực hiện rút gọn phân thức
Lời giải chi tiết:
Ta có:\(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{2{\rm{x}}}}{{x + 1}}\)
Video hướng dẫn giải
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Phương pháp giải:
Dựa vào tính chất cơ bàn của phân thức
Lời giải chi tiết:
Ta có: \(\frac{{x - y}}{{{x^3} - {y^3}}} = \frac{{x - y}}{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{1}{{{x^2} + xy + {y^2}}}\)
Video hướng dẫn giải
Thực hiện rút gọn một phân thức như hình bên . Hỏi bạn tròn làm đúng hay sai/ Vì sao?
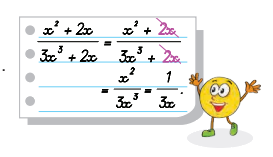
Phương pháp giải:
Dựa vào cách rút gọn một phân thức
Lời giải chi tiết:
Bạn tròn làm thế là sai. Vì bạn bỏ hai số hạng giống nhau của cả tử và mẫu là 2x chứ không phải chia cho nhân tử chung của cả tử và mẫu.
Video hướng dẫn giải
Tìm a sao cho hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\)
Phương pháp giải:
Áp dụng quy tắc rút gọn phân thức
Lời giải chi tiết:
Ta có: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}} = \frac{{ - a\left( {{x^2} + x} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{ - ax\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{{\rm{ - ax}}}}{{x - 1}}\)
Để hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\) khi và chỉ khi a = -3
Video hướng dẫn giải
Cho hai phân thức: \(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}}\)và \(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}}\). Phân tích các mẫu thức của hai phân thức đã cho thành nhân tử
Phương pháp giải:
Phân tích mẫu thức của mỗi phân thức theo phân tích đa thức thành nhân tử
Lời giải chi tiết:
Ta có: \(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}} = \frac{1}{{2{\rm{x}}\left( {x + 1} \right)}}\)
\(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}} = \frac{1}{{3{\rm{x}}\left( {x - 2} \right)}}\)
Video hướng dẫn giải
Chọn mẫu thức chung (MTC) của hai mẫu thức trên bàng cách lấy tích của các nhân tử được chọn như sau:
- Nhân tử bằng số của MTC là tích các nhân tử bằng số ở các mẫu thức của các phân thức đã cho (nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử bằng số ở MTC là BCNN của chúng);
- Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa với số mũ cao nhất.
Phương pháp giải:
Thực hiện theo yêu cầu của đề bài
Lời giải chi tiết:
Mẫu thức chung: 6x(x+1)(x−2)
Video hướng dẫn giải
Tìm nhân tử phụ của mỗi mẫu thức bằng cách lấy MTC chia cho mẫu thức đó
Phương pháp giải:
Lấy MTC chia cho mẫu của mỗi phân thức
Lời giải chi tiết:
Nhân tử phụ của 2x2 +2x là 3(x−2)
Nhân tử phụ của 3x2 −6x là 2(x+1)
Video hướng dẫn giải
Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng, ta được các phân thức có mẫu thức là MTC đã chọn
Phương pháp giải:
Thực hiện theo yêu cầu của đề bài
Lời giải chi tiết:
Ta có:\(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}} = \frac{1}{{2{\rm{x}}\left( {x + 1} \right)}} = \frac{{3{\rm{x}}\left( {x - 2} \right)}}{{6{\rm{x}}\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}} = \frac{1}{{3{\rm{x}}\left( {x - 2} \right)}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{6{\rm{x}}\left( {x + 1} \right)\left( {x - 2} \right)}}\)
Video hướng dẫn giải
Quy đồng mẫu thức hai phân thức \(\frac{1}{{3{{\rm{x}}^2} - 3}}\) và \(\frac{1}{{{x^3} - 1}}\)
Phương pháp giải:
- Phân tích mẫu của hai phân thức đã cho
- Tìm MTC
- Tìm nhân tử phụ của mỗi mẫu thức
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ
Lời giải chi tiết:
Ta có:3x2 −3=3(x2−1)=3(x−1)(x+1)
x3 −1=(x−1)(x2 + x + 1)
MTC= 3(x−1)(x+1)(x2 + x + 1)
Nhân tử phụ của 3x2 − 3 là x2 + x + 1
Nhân tử phụ của x3 − 1 là 3(x+1)
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có:
\(\frac{1}{{3{{\rm{x}}^2} - 3}} = \frac{{{x^2} + x + 1}}{{3\left( {{x^2} - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{{x^2} + x + 1}}{{3\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\(\frac{1}{{{x^3} - 1}} = \frac{{3\left( {x + 1} \right)}}{{3\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)}}\)
Video hướng dẫn giải
Tròn: hai phân thức \(\frac{5}{{x - 1}}\) và \(\frac{x}{{1 - x}}\) có MTC là x – 1
Vuông: Không đúng, MTC là (x – 1)(1 – x)
Theo em, bạn nào chọn MTC hợp lí hơn? Vì sao?
Phương pháp giải:
Nhân cả tử và mẫu của phân thức \(\frac{5}{{x - 1}}\) với -1
Lời giải chi tiết:
Ta có: \(\frac{x}{{1 - x}} = \frac{{ - x}}{{x - 1}}\)
Hai phân thức \(\frac{5}{{x - 1}}\) và \(\frac{x}{{1 - x}}\) có MTC là x – 1
Bạn Tròn chọn MTC hợp lí hơn.
Mục 2 của SGK Toán 8 tập 2 Kết nối tri thức xoay quanh các kiến thức về tứ giác, bao gồm các loại tứ giác đặc biệt như hình thang, hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc nắm vững định nghĩa, tính chất và dấu hiệu nhận biết của từng loại tứ giác là vô cùng quan trọng để giải quyết các bài tập liên quan.
Để giải tốt các bài tập trong Mục 2, các em cần:
Bài 1: (Trang 9) Cho tứ giác ABCD. Biết tổng ba góc A, B, C bằng 260 độ. Tính góc D.
Lời giải:
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
A + B + C + D = 360 độ
=> 260 độ + D = 360 độ
=> D = 360 độ - 260 độ = 100 độ
Vậy, góc D bằng 100 độ.
Bài 2: (Trang 10) Cho hình thang ABCD (AB // CD). Biết góc A = 60 độ, góc C = 120 độ. Tính các góc B và D.
Lời giải:
Vì AB // CD, ta có:
A + D = 180 độ => D = 180 độ - A = 180 độ - 60 độ = 120 độ
B + C = 180 độ => B = 180 độ - C = 180 độ - 120 độ = 60 độ
Vậy, góc B bằng 60 độ và góc D bằng 120 độ.
Bài 3: (Trang 11) Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Chứng minh rằng DE là phân giác của góc ADC.
Lời giải:
Vì ABCD là hình bình hành, ta có:
AD // BC và AB // CD
=> Góc ADC = góc ABC (các góc đối nhau trong hình bình hành bằng nhau)
Vì E là trung điểm của AB, ta có AE = EB
Xét tam giác ADE và tam giác BCE, ta có:
AE = BC (vì AB = CD và AE = 1/2 AB)
Góc DAE = góc BCE (so le trong do AD // BC)
AD = BE (cạnh đối nhau trong hình bình hành)
=> Tam giác ADE = tam giác BCE (c.g.c)
=> Góc ADE = góc BCE
=> DE là phân giác của góc ADC (vì góc ADE = góc CDE)
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về các kiến thức và phương pháp giải bài tập trong Mục 2 SGK Toán 8 tập 2 Kết nối tri thức. Chúc các em học tập tốt!