Chào mừng bạn đến với bài học về Lý thuyết Hiệu hai bình phương và Bình phương của một tổng hay một hiệu, một trong những kiến thức quan trọng của chương trình Toán 8 - Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản, công thức quan trọng và các ví dụ minh họa để bạn có thể hiểu rõ và áp dụng vào giải bài tập.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và phù hợp với mọi trình độ học sinh.
Hằng đẳng thức là gì?
Hằng đẳng thức:
Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.
Ví dụ: \(a + b = b + a;a(a + 2) = {a^2} + 2a\) là những hằng đẳng thức.
\({a^2} - 1 = 3a;a(a - 1) = 2a\) không phải là những hằng đẳng thức.
Hiệu hai bình phương là gì?
\({A^2} - {B^2} = (A - B)(A + B)\)
Ví dụ: \({101^2} - {99^2} = (101 - 99)(101 + 99) = 2.200 = 400\)
Bình phương của một tổng:
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Ví dụ: \({101^2} = {(100 + 1)^2} = {100^2} + 2.100.1 + {1^2} = 10201\)
Bình phương của một hiệu:
\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Ví dụ: \({99^2} = {(100 - 1)^2} = {100^2} - 2.100.1 + {1^2} = 9801\)
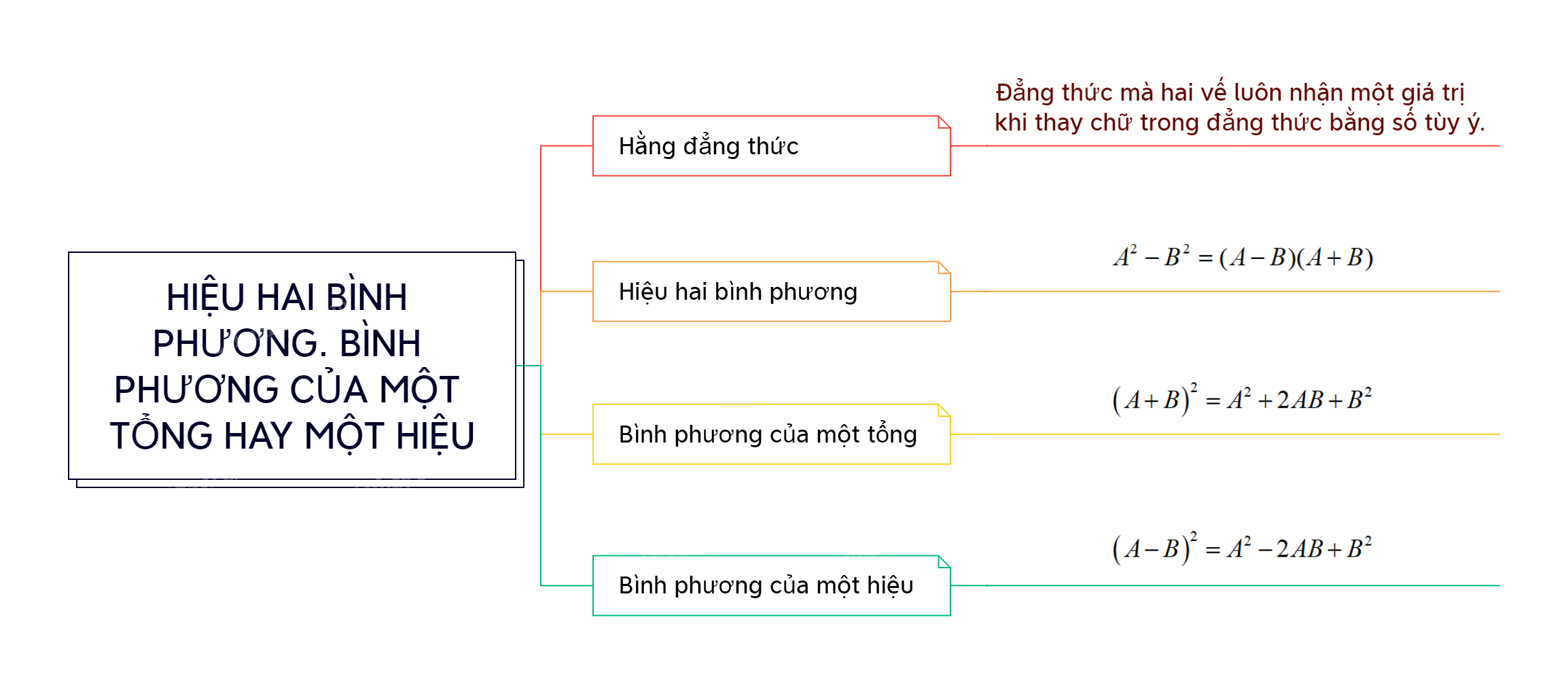
Trong chương trình Toán 8, kiến thức về các hằng đẳng thức đáng nhớ đóng vai trò vô cùng quan trọng. Trong đó, Hiệu hai bình phương và Bình phương của một tổng hay một hiệu là những hằng đẳng thức cần được nắm vững để giải quyết các bài toán đại số một cách hiệu quả.
Phát biểu: Với hai biểu thức A và B, ta có:
A2 - B2 = (A - B)(A + B)
Ví dụ:
Ứng dụng: Hiệu hai bình phương thường được sử dụng để phân tích đa thức thành nhân tử, giải các phương trình bậc hai và đơn giản hóa các biểu thức đại số.
Phát biểu: Với hai biểu thức A và B, ta có:
(A + B)2 = A2 + 2AB + B2
Ví dụ:
Ứng dụng: Bình phương của một tổng được sử dụng để khai triển biểu thức, giải các phương trình bậc hai và chứng minh các đẳng thức.
Phát biểu: Với hai biểu thức A và B, ta có:
(A - B)2 = A2 - 2AB + B2
Ví dụ:
Ứng dụng: Bình phương của một hiệu được sử dụng để khai triển biểu thức, giải các phương trình bậc hai và chứng minh các đẳng thức.
Để hiểu rõ hơn về các hằng đẳng thức trên, chúng ta hãy cùng giải một số bài tập sau:
Các hằng đẳng thức trên không chỉ áp dụng cho các biểu thức đơn giản mà còn có thể được mở rộng cho các biểu thức phức tạp hơn. Khi áp dụng, cần chú ý đến dấu và thứ tự thực hiện các phép toán để tránh sai sót.
Việc nắm vững các hằng đẳng thức này là nền tảng quan trọng để học tốt môn Toán ở các lớp trên. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.
Bài học hôm nay đã cung cấp cho bạn những kiến thức cơ bản về Hiệu hai bình phương và Bình phương của một tổng hay một hiệu. Hy vọng rằng, với những kiến thức này, bạn sẽ tự tin hơn trong việc giải các bài toán Toán 8 và các bài toán liên quan.