Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 88, 89 SGK Toán 8 tập 2 - Kết nối tri thức trên giaitoan.edu.vn.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ gia sư giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải bài tập Toán 8 tập 2 đầy đủ, chính xác, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Bạn Tròn đang đứng ở vị trí điểm A
Video hướng dẫn giải
Nếu ΔABC∽ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét?
Phương pháp giải:
Dựa vào tỉ số đồng dạng của hai tam giác, tính khoảng cách từ bạn Tròn đến chân cột cờ.
Lời giải chi tiết:
Có ΔA'B'C' ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{5}\)
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{5}\)
mà A′C′=3,76 (m) => AC=18,8 (m)
Khoảng cách từ bạn Tròn đến chân cột cờ là 18,8 m.
Video hướng dẫn giải
1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu \( \widehat {A'I'B'} = \widehat {AIB} \) và \( \widehat {A'I'C'} = \widehat {AIC} \) thì \( \Delta A'B'C' \backsim \Delta ABC \).
2. Với hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giả thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không?
Phương pháp giải:
1. Chứng minh tam giác ABC và tam giác A'B'C' đồng dạng theo trường hợp góc - góc.
2. Tương tự như phần Tranh luận, lấy điểm M trên tia BC sao cho \( \Delta ABM \backsim \Delta A'B'C' \). Giả sử điểm C không trùng với M và chứng minh điều đó là vô lý => Điểm C phải trùng với M và \( \Delta A'B'C' \backsim \Delta ABC \)
Lời giải chi tiết:
1. Do tổng các góc trong một tam giác bằng $180^{\circ}$ nên:
$\frac{\widehat{A^{\prime}}+\widehat{B^{\prime}}}{2}=180^{\circ}-\widehat{A^{\prime} I^{\prime} B^{\prime}}=180^{\circ}-\widehat{A I B}=\frac{\widehat{A}+\widehat{B}}{2} \text {. }$
Suy ra $\widehat{A^{\prime}}+\widehat{B^{\prime}}=\widehat{A}+\widehat{B}$. Do đó $\widehat{C^{\prime}}=180^{\circ}-\widehat{A^{\prime}}-\widehat{B^{\prime}}=180^{\circ}-\widehat{A}-\widehat{B}=\widehat{C} \text {. } $
Tương tự, $\widehat{B^{\prime}}=\widehat{B}$. Vậy $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B C$ có: $\widehat{B^{\prime}}=\widehat{B}, \widehat{C^{\prime}}=\widehat{C}$. Do đó $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$ (g.g).
2. Nếu góc C và C' đều nhọn: Lấy điểm $M$ trên tia $B C$ sao cho $\triangle A B M \perp \triangle A^{\prime} B^{\prime} C^{\prime}$. Giả sử điểm $C$ không trùng với $M$. Khi đó: $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B M$ nên $\frac{A^{\prime} C^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}$ và kéo theo $A M=A C$, hay $\triangle A M C$ cân tại $A$.
+) Nếu $M$ nằm giữa $B$ và $C$ thì $\widehat{A M B}=180^{\circ}-\widehat{A M C}$
$=180^{\circ}-\widehat{A C M}>90^{\circ}>\widehat{A^{\prime} C^{\prime} M^{\prime}}$ và ta nhận được điều vô lí.
+) Vậy $C$ ở giữa $B$ và $M$ (như hình 9.19). Khi đó $\widehat{A C B}=180^{\circ}-\widehat{A C M}$
$=180^{\circ}-\widehat{A M B}=180^{\circ}-\widehat{C}>90^{\circ}$ và ta nhận được điều vô lí.
Vậy điểm $C$ phải trùng với $M$ và $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$.
Video hướng dẫn giải
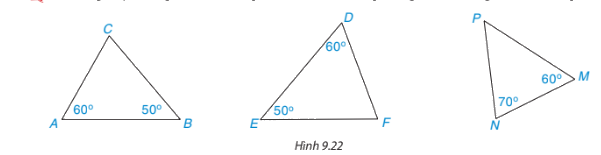
Những cặp tam giác nào trong hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng
Phương pháp giải:
Quan sát hình 9.22 và vận dụng trường hợp đồng dạng thứ ba của tam giác
Lời giải chi tiết:
Xét tam giác MPN có: \(\widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {60^o} - {70^o} = {50^o}\)
Các cặp tam giác đồng dạng trong hình 9.22 là: \(\Delta ACB \backsim \Delta DF{\rm{E; }}\Delta {\rm{ACB}} \backsim \Delta {\rm{MP}}N;\Delta DF{\rm{E}} \backsim \Delta MPN\)
Video hướng dẫn giải
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, \(\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}\) và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, \(\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}\)(H.9.20b)
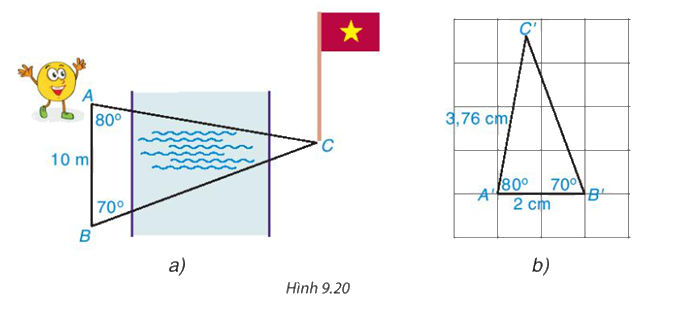
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu
Phương pháp giải:
Quan sát hình 9.20 để trả lời câu hỏi.
Lời giải chi tiết:
Đổi 10m = 1000cm
Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng \(\frac{A'B'}{AB} = \frac{2}{1000} = \frac{1}{500}\)
Video hướng dẫn giải
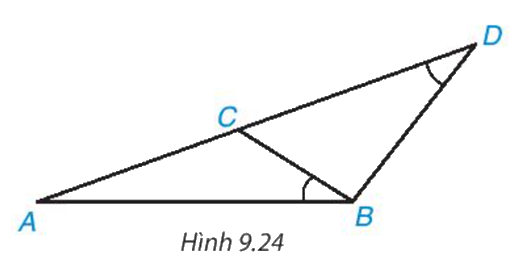
Cho các điểm A, B, C, D như Hình 9.24. Biết rằng \(\widehat {ABC} = \widehat {A{\rm{D}}B}\). Hãy chứng minh ΔABC∽ΔADB và \(A{B^2} = A{\rm{D}}.AC\)
Phương pháp giải:
Chứng minh ΔABC ∽ ΔADB (g.g) suy ra tỉ số đồng dạng
Lời giải chi tiết:
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)
Video hướng dẫn giải
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, \(\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}\) và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, \(\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}\)(H.9.20b)
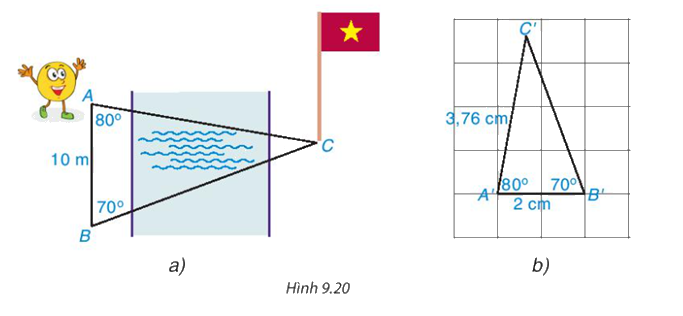
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu
Phương pháp giải:
Quan sát hình 9.20 để trả lời câu hỏi.
Lời giải chi tiết:
Đổi 10m = 1000cm
Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng \(\frac{A'B'}{AB} = \frac{2}{1000} = \frac{1}{500}\)
Video hướng dẫn giải
Nếu ΔABC∽ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét?
Phương pháp giải:
Dựa vào tỉ số đồng dạng của hai tam giác, tính khoảng cách từ bạn Tròn đến chân cột cờ.
Lời giải chi tiết:
Có ΔA'B'C' ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{5}\)
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{5}\)
mà A′C′=3,76 (m) => AC=18,8 (m)
Khoảng cách từ bạn Tròn đến chân cột cờ là 18,8 m.
Video hướng dẫn giải
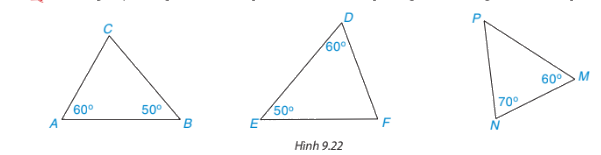
Những cặp tam giác nào trong hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng
Phương pháp giải:
Quan sát hình 9.22 và vận dụng trường hợp đồng dạng thứ ba của tam giác
Lời giải chi tiết:
Xét tam giác MPN có: \(\widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {60^o} - {70^o} = {50^o}\)
Các cặp tam giác đồng dạng trong hình 9.22 là: \(\Delta ACB \backsim \Delta DF{\rm{E; }}\Delta {\rm{ACB}} \backsim \Delta {\rm{MP}}N;\Delta DF{\rm{E}} \backsim \Delta MPN\)
Video hướng dẫn giải
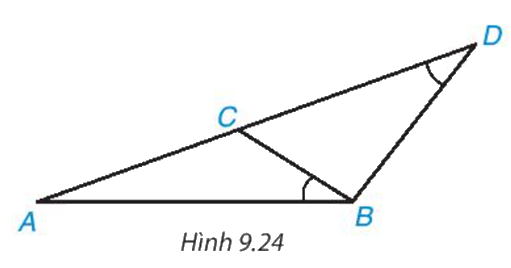
Cho các điểm A, B, C, D như Hình 9.24. Biết rằng \(\widehat {ABC} = \widehat {A{\rm{D}}B}\). Hãy chứng minh ΔABC∽ΔADB và \(A{B^2} = A{\rm{D}}.AC\)
Phương pháp giải:
Chứng minh ΔABC ∽ ΔADB (g.g) suy ra tỉ số đồng dạng
Lời giải chi tiết:
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)
Video hướng dẫn giải
1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu \( \widehat {A'I'B'} = \widehat {AIB} \) và \( \widehat {A'I'C'} = \widehat {AIC} \) thì \( \Delta A'B'C' \backsim \Delta ABC \).
2. Với hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giả thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không?
Phương pháp giải:
1. Chứng minh tam giác ABC và tam giác A'B'C' đồng dạng theo trường hợp góc - góc.
2. Tương tự như phần Tranh luận, lấy điểm M trên tia BC sao cho \( \Delta ABM \backsim \Delta A'B'C' \). Giả sử điểm C không trùng với M và chứng minh điều đó là vô lý => Điểm C phải trùng với M và \( \Delta A'B'C' \backsim \Delta ABC \)
Lời giải chi tiết:
1. Do tổng các góc trong một tam giác bằng $180^{\circ}$ nên:
$\frac{\widehat{A^{\prime}}+\widehat{B^{\prime}}}{2}=180^{\circ}-\widehat{A^{\prime} I^{\prime} B^{\prime}}=180^{\circ}-\widehat{A I B}=\frac{\widehat{A}+\widehat{B}}{2} \text {. }$
Suy ra $\widehat{A^{\prime}}+\widehat{B^{\prime}}=\widehat{A}+\widehat{B}$. Do đó $\widehat{C^{\prime}}=180^{\circ}-\widehat{A^{\prime}}-\widehat{B^{\prime}}=180^{\circ}-\widehat{A}-\widehat{B}=\widehat{C} \text {. } $
Tương tự, $\widehat{B^{\prime}}=\widehat{B}$. Vậy $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B C$ có: $\widehat{B^{\prime}}=\widehat{B}, \widehat{C^{\prime}}=\widehat{C}$. Do đó $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$ (g.g).
2. Nếu góc C và C' đều nhọn: Lấy điểm $M$ trên tia $B C$ sao cho $\triangle A B M \perp \triangle A^{\prime} B^{\prime} C^{\prime}$. Giả sử điểm $C$ không trùng với $M$. Khi đó: $\triangle A^{\prime} B^{\prime} C^{\prime}$ và $\triangle A B M$ nên $\frac{A^{\prime} C^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}$ và kéo theo $A M=A C$, hay $\triangle A M C$ cân tại $A$.
+) Nếu $M$ nằm giữa $B$ và $C$ thì $\widehat{A M B}=180^{\circ}-\widehat{A M C}$
$=180^{\circ}-\widehat{A C M}>90^{\circ}>\widehat{A^{\prime} C^{\prime} M^{\prime}}$ và ta nhận được điều vô lí.
+) Vậy $C$ ở giữa $B$ và $M$ (như hình 9.19). Khi đó $\widehat{A C B}=180^{\circ}-\widehat{A C M}$
$=180^{\circ}-\widehat{A M B}=180^{\circ}-\widehat{C}>90^{\circ}$ và ta nhận được điều vô lí.
Vậy điểm $C$ phải trùng với $M$ và $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$.
Mục 3 trang 88, 89 SGK Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Nội dung chính bao gồm việc nhắc lại các kiến thức về góc so le trong, góc đồng vị, góc trong cùng phía, góc ngoài tại đỉnh của một tam giác, và các tính chất liên quan. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn trong chương trình học.
Bài tập trong mục này thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh quan sát hình vẽ và xác định các cặp góc so le trong, góc đồng vị, góc trong cùng phía. Để giải bài này, học sinh cần nắm vững định nghĩa của các loại góc này và biết cách nhận biết chúng trong hình vẽ.
Ví dụ: Nếu đường thẳng a cắt hai đường thẳng b và c, và góc tạo bởi a và b nằm bên trong hai đường thẳng b và c, đồng thời ở phía đối diện với một góc khác tạo bởi a và c, thì hai góc đó là góc so le trong.
Bài 2 thường yêu cầu học sinh tính số đo góc dựa trên các tính chất đã học. Ví dụ, nếu hai đường thẳng song song, thì góc so le trong bằng nhau, góc đồng vị bằng nhau, góc trong cùng phía bù nhau.
Để giải bài này, học sinh cần xác định được các cặp góc có mối quan hệ với nhau và vận dụng các tính chất tương ứng để tính toán.
Bài 3 thường là bài toán chứng minh hai đường thẳng song song. Để chứng minh hai đường thẳng song song, học sinh có thể sử dụng các điều kiện sau:
Học sinh cần phân tích đề bài, tìm ra các yếu tố liên quan đến các điều kiện trên và sử dụng chúng để chứng minh.
Để học tốt môn Toán 8, đặc biệt là phần hình học, học sinh nên:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mục 3 trang 88, 89 SGK Toán 8 tập 2 - Kết nối tri thức trên giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong việc học Toán 8. Chúc các em học tập tốt!