Chào mừng bạn đến với bài học lý thuyết về phép nhân và phép chia phân thức đại số lớp 8, thuộc chương trình Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng, các quy tắc quan trọng và ví dụ minh họa để bạn có thể hiểu rõ và vận dụng thành thạo vào giải bài tập.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả và thú vị. Hãy cùng bắt đầu khám phá thế giới của phân thức đại số!
Nhân hai đa thức như thế nào?
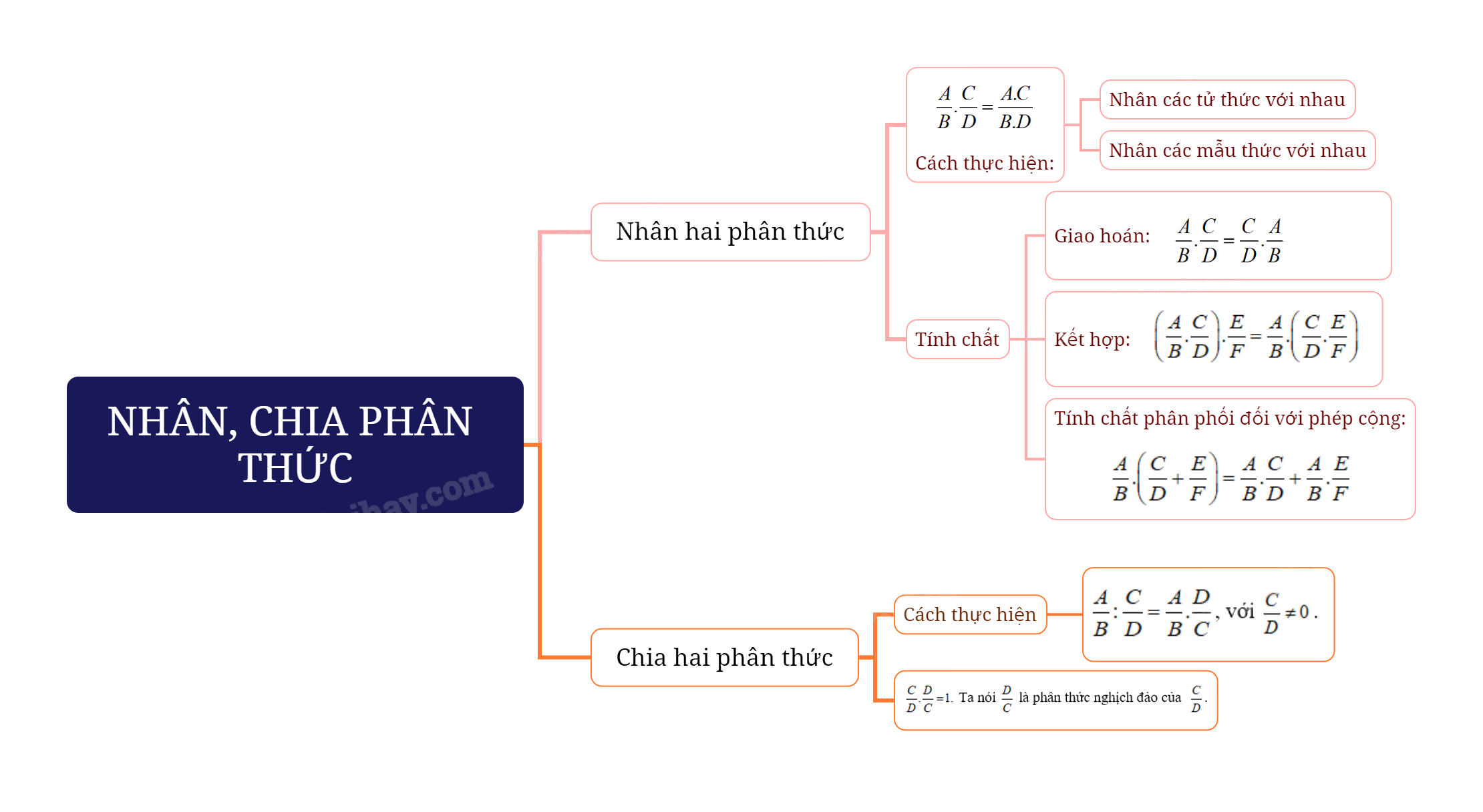
1. Nhân hai phân thức
Quy tắc: Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau.
\(\frac{A}{B}.\frac{C}{D} = \frac{{A.C}}{{B.D}}\)
Chú ý: Kết quả của phép nhân hai phân thức được gọi là tích. Ta thường viết tích dưới dạng rút gọn.
2. Tính chất của phép nhân phân thức
- Giao hoán: \(\frac{A}{B}.\frac{C}{D} = \frac{C}{D}.\frac{A}{B}\)
- Kết hợp: \(\left( {\frac{A}{B}.\frac{C}{D}} \right).\frac{E}{F} = \frac{A}{B}.\left( {\frac{C}{D}.\frac{E}{F}} \right)\)
- Tính chất phân phối đối với phép cộng: \(\frac{A}{B}.\left( {\frac{C}{D} + \frac{E}{F}} \right) = \frac{A}{B}.\frac{C}{D} + \frac{A}{B}.\frac{E}{F}\)
Ví dụ:
\(\frac{{2xz}}{{3y}}.\frac{{ - 6{y^3}}}{{8{x^2}z}} = \frac{{2xz.( - 6{y^3})}}{{3y.8{x^2}z}} = \frac{{ - {y^2}}}{{2x}}\);
\(\frac{{{x^2} - 1}}{{{x^2} + 4x}}.\frac{{2x}}{{x - 1}} = \frac{{(x - 1)(x + 1).2x}}{{x(x + 4)(x - 1)}} = \frac{{2(x + 1)}}{{x + 4}}\)
3. Chia hai phân thức
Quy tắc: Muốn chia phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\) khác 0, ta nhân phân thức \(\frac{A}{B}\) với phân thức \(\frac{D}{C}\):
\(\frac{A}{B}:\frac{C}{D} = \frac{A}{B}.\frac{D}{C}\), với \(\frac{C}{D} \ne 0\).
Nhận xét: \(\frac{C}{D}.\frac{D}{C} = 1.\) Ta nói \(\frac{D}{C}\) là phân thức nghịch đảo của \(\frac{C}{D}\).
Ví dụ:
1)
\(\frac{{{x^2} - 9}}{{x - 2}}:\frac{{x - 3}}{x} \\= \frac{{(x - 3)(x + 3)}}{{x - 2}}.\frac{x}{{x - 3}} \\= \frac{{(x - 3)(x + 3).x}}{{(x - 2)(x - 3)}} \\= \frac{{x(x + 3)}}{{x - 2}}\)
2)
\(\frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}:\frac{{{x^3}}}{{yz}} \\= \frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}.\frac{{yz}}{{{x^3}}} \\= \frac{{x.xz.yz}}{{{z^2}.{y^3}.{x^3}}} \\= \frac{{{x^2}y{z^2}}}{{{x^3}{y^3}{z^2}}} \\= \frac{1}{{x{y^2}}}\)
Phân thức đại số là một khái niệm quan trọng trong chương trình Toán học lớp 8, đặc biệt là trong chương trình Kết nối tri thức. Để nắm vững kiến thức này, việc hiểu rõ lý thuyết về phép nhân và phép chia phân thức là vô cùng cần thiết. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, kèm theo các ví dụ minh họa và bài tập vận dụng.
Một phân thức đại số là một biểu thức có dạng P(x) / Q(x), trong đó P(x) là đa thức ở tử và Q(x) là đa thức ở mẫu. Điều kiện xác định của phân thức là Q(x) ≠ 0.
Để nhân hai phân thức đại số, ta thực hiện theo quy tắc sau:
Công thức tổng quát:
A/B * C/D = (A*C) / (B*D)
Tính (x + 1) / (x - 2) * (x - 3) / (x + 1)
Giải:
(x + 1) / (x - 2) * (x - 3) / (x + 1) = (x + 1)(x - 3) / (x - 2)(x + 1) = (x - 3) / (x - 2) (với x ≠ -1)
Để chia hai phân thức đại số, ta thực hiện theo quy tắc sau:
Công thức tổng quát:
A/B : C/D = A/B * D/C = (A*D) / (B*C)
Tính (x + 2) / (x - 1) : (x - 3) / (x + 2)
Giải:
(x + 2) / (x - 1) : (x - 3) / (x + 2) = (x + 2) / (x - 1) * (x + 2) / (x - 3) = (x + 2)(x + 2) / (x - 1)(x - 3) (với x ≠ 1, x ≠ 3)
Hãy tự giải các bài tập sau để củng cố kiến thức:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết phép nhân và phép chia phân thức đại số lớp 8 - Kết nối tri thức. Chúc bạn học tập tốt!