Chào mừng bạn đến với bài học về Lý thuyết Lập phương của một tổng hay một hiệu, một phần quan trọng trong chương trình Toán 8 - Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản về công thức, cách áp dụng và các bài tập minh họa để bạn có thể nắm vững kiến thức này một cách dễ dàng.
Giaitoan.edu.vn tự hào là địa chỉ học toán online uy tín, cung cấp nội dung chất lượng và phương pháp học tập hiệu quả.
Lập phương của một tổng là gì?
Lập phương của một tổng:
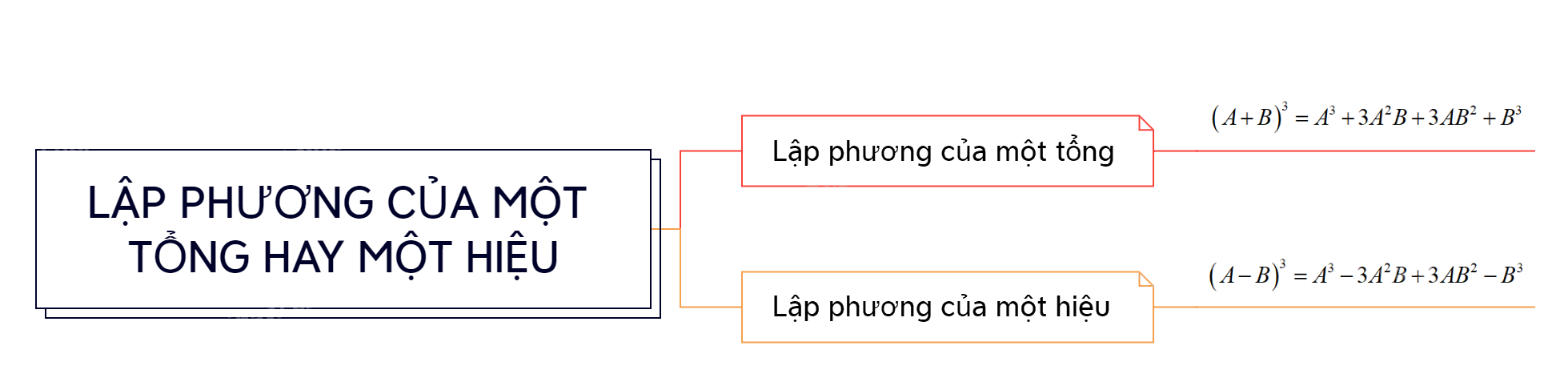
\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
Ví dụ: \({\left( {x + 3} \right)^3} = {x^3} + 3{x^2}.3 + 3x{.3^2} + {3^3} = {x^3} + 9{x^2} + 27x + 27\)
Lập phương của một hiệu:
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Ví dụ: \({\left( {x - 3} \right)^3} = {x^3} - 3{x^2}.3 + 3x{.3^2} - {3^3} = {x^3} - 9{x^2} + 27x - 27\)
Trong chương trình Toán 8, việc nắm vững các hằng đẳng thức đại số là vô cùng quan trọng. Một trong những hằng đẳng thức quan trọng nhất là công thức lập phương của một tổng và một hiệu. Bài viết này sẽ trình bày chi tiết về lý thuyết này, kèm theo các ví dụ minh họa và bài tập vận dụng để giúp bạn hiểu rõ hơn.
Công thức lập phương của một tổng được phát biểu như sau:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Công thức này cho biết cách khai triển biểu thức (a + b)3 thành tổng của các đơn thức. Để nhớ công thức này một cách dễ dàng, bạn có thể sử dụng quy tắc “1, 3, 3, 1” với các lũy thừa của a và b.
Công thức lập phương của một hiệu được phát biểu như sau:
(a - b)3 = a3 - 3a2b + 3ab2 - b3
Tương tự như công thức lập phương của một tổng, công thức này cho biết cách khai triển biểu thức (a - b)3 thành hiệu của các đơn thức. Lưu ý rằng các dấu trong công thức lập phương của một hiệu xen kẽ nhau.
Ví dụ 1: Khai triển biểu thức (x + 2)3
Áp dụng công thức lập phương của một tổng, ta có:
(x + 2)3 = x3 + 3x2(2) + 3x(22) + 23 = x3 + 6x2 + 12x + 8
Ví dụ 2: Khai triển biểu thức (y - 1)3
Áp dụng công thức lập phương của một hiệu, ta có:
(y - 1)3 = y3 - 3y2(1) + 3y(12) - 13 = y3 - 3y2 + 3y - 1
Công thức lập phương của một tổng và một hiệu có nhiều ứng dụng trong việc giải toán, đặc biệt là trong các bài toán về rút gọn biểu thức, chứng minh đẳng thức và giải phương trình. Việc nắm vững công thức này sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và hiệu quả.
Ngoài công thức lập phương của một tổng và một hiệu, còn có các công thức khác liên quan đến hằng đẳng thức đại số, như công thức lập phương của một hiệu, công thức tổng và hiệu hai lập phương. Việc tìm hiểu và nắm vững các công thức này sẽ giúp bạn có một nền tảng toán học vững chắc.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Lập phương của một tổng hay một hiệu SGK Toán 8 - Kết nối tri thức. Chúc bạn học tập tốt!