Chào mừng bạn đến với bài học lý thuyết về Khái niệm hàm số và đồ thị của hàm số trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hàm số, bao gồm định nghĩa, các loại hàm số đơn giản và cách biểu diễn hàm số bằng đồ thị.
Hàm số là gì?
1. Hàm số
Khái niệm:
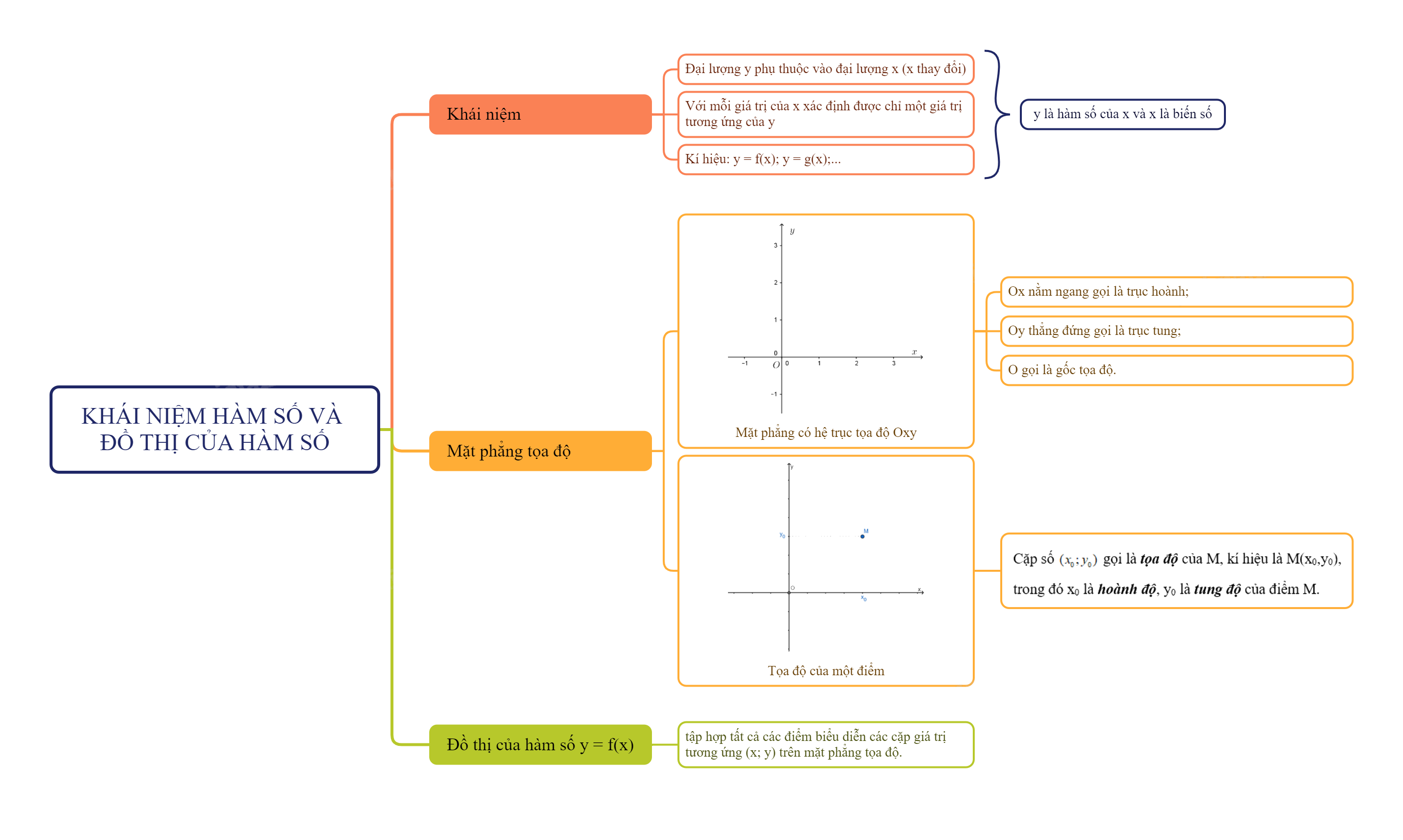
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.
t(h) | 10 | 11 | 12 | 13 |
T(0C) | 32 | 33 | 34 | 34 |
Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.
Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 340C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.
Chú ý: Khi y là hàm số của x, ta viết \(y = f(x);y = g(x),...\)
Ví dụ: Cho hàm số y = f(x) = x + 3.
f(-2) = -2 + 3 = 1; f(0) = 0 + 3 = 3
2. Mặt phẳng tọa độ
Khái niệm: Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ.
Tọa độ của một điểm:
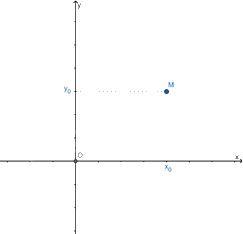
Trong mặt phẳng tọa độ, mỗi điểm M xác định duy nhất một cặp số \(({x_0};{y_0})\) và mỗi cặp số \(({x_0};{y_0})\) xác định duy nhất một điểm M.
Cặp số \(({x_0};{y_0})\) gọi là tọa độ của M, kí hiệu là M(x0,y0), trong đó x0 là hoành độ, y0 là tung độ của điểm M.
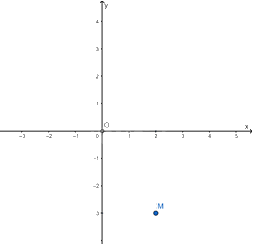
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng tọa độ.
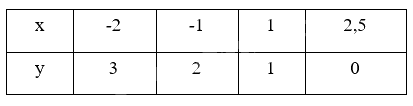
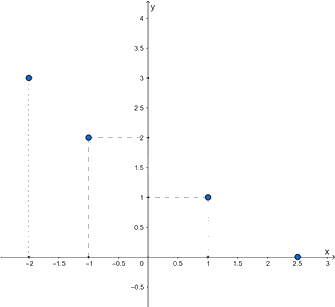
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng:
Hàm số là một khái niệm nền tảng trong toán học, đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau. Việc hiểu rõ về hàm số và đồ thị hàm số là điều cần thiết để các em học sinh lớp 8 có thể tiếp thu tốt các kiến thức toán học ở các lớp trên.
Một hàm số là một quy tắc tương ứng, mỗi phần tử của tập hợp A (tập xác định) với duy nhất một phần tử của tập hợp B (tập giá trị). Ký hiệu: y = f(x), trong đó x thuộc A, y thuộc B.
Trong chương trình Toán 8, các em sẽ được làm quen với một số loại hàm số đơn giản sau:
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm trên mặt phẳng tọa độ có tọa độ (x; f(x)) với mọi x thuộc tập xác định của hàm số.
Cách vẽ đồ thị hàm số:
Ví dụ 1: Vẽ đồ thị hàm số y = 2x + 1
Ta có:
| x | y = 2x + 1 |
|---|---|
| -2 | -3 |
| -1 | -1 |
| 0 | 1 |
| 1 | 3 |
Biểu diễn các điểm (-2; -3), (-1; -1), (0; 1), (1; 3) lên mặt phẳng tọa độ và nối chúng lại, ta được đồ thị hàm số y = 2x + 1.
Ví dụ 2: Xác định tập xác định của hàm số y = 1/(x-2)
Hàm số y = 1/(x-2) xác định khi và chỉ khi mẫu số khác 0, tức là x - 2 ≠ 0, suy ra x ≠ 2. Vậy tập xác định của hàm số là D = R \ {2}.
Để củng cố kiến thức về khái niệm hàm số và đồ thị hàm số, các em hãy làm các bài tập sau:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về khái niệm hàm số và đồ thị hàm số. Chúc các em học tốt!