Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 8 tập 2 Kết nối tri thức, đặc biệt là các bài tập trang 104, 105, 106, 107.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
Lấy điểm O và vẽ tam giác A'B'C' như Hình 9.58.
Video hướng dẫn giải
Theo em, hai hình tam giác bằng nhau có phải là hai hình đồng dạng phối cảnh không?
Phương pháp giải:
Dựa vào khái niệm hình đồng dạng, hình đồng dạng phối cảnh.
Lời giải chi tiết:
Hai tam giác bằng nhau không phải là hình đồng dạng phối cảnh
Video hướng dẫn giải
Vuông: Tớ nghĩ là hai hình vuông bất kì đều đồng dạng với nhau
Tròn: Tớ nghĩ hai hình tam giác đều bất kì đồng dạng phối cảnh với nhau
Theo em, bạn nào nói đúng, bạn nào nói sai? Cho biết ý kiến của em?
Phương pháp giải:
Dựa vào khái niệm hình đồng dạng, hình đồng dạng phối cảnh
Lời giải chi tiết:
Theo em, bạn Vuông nói đúng, bạn tròn nói sai
Video hướng dẫn giải
Lấy điểm O và vẽ tam giác A'B'C' như Hình 9.58. Trên các tia OA', OB', OC', lấy các điểm A, B, C sao cho OA = 2OA', OB = 2OB', OC = 2OC'
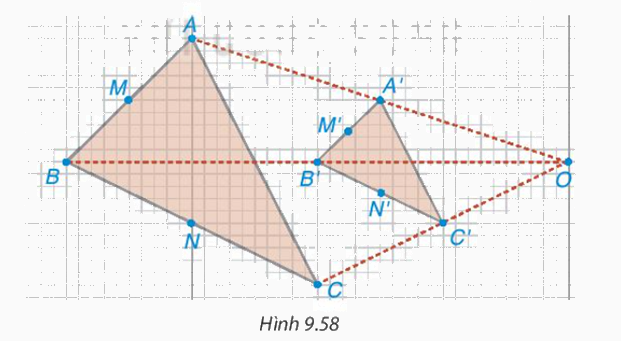
- Hãy giải thích vì sao ΔABC ∽ ΔA'B'C' với tỉ số đồng dạng bằng 2
- Dùng thước thẳng, em hãy kiểm tra xem đường thẳng MM', NN' nối các trung điểm có đi qua O không?
Trong Hình 9.58, ta nói tam giác ABC là hình phóng to (2 lần) của tam giác A'B'C' và tam giác A'B'C' là hình thu nhỏ (2 lần) của tam giác ABC
Phương pháp giải:
Vì ΔOA'B' ∽ ΔOAB (c.g.c) và ΔOB'C' ∽ ΔOBC(c.g.c) nên ΔABC ∽ ΔA'B'C' (c.g.c)
Lời giải chi tiết:
- Có \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOA'B' ∽ ΔOAB (c.g.c)
- Có \(\frac{{OC'}}{{OC}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOB'C' ∽ ΔOBC(c.g.c)
=> ΔABC ∽ ΔA'B'C' (c.g.c)
- Đường thẳng có đi qua O
Video hướng dẫn giải
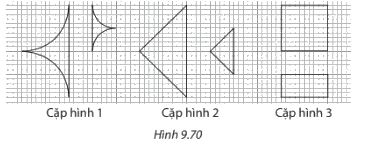
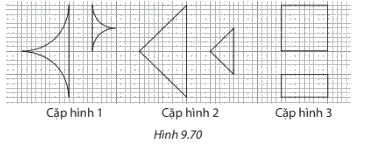
Trong những cặp hình dưới đây (H.9.70), cặp hình nào là hai hình đồng dạng? Hãy chỉ ra một cặp hình đồng dạng phối cảnh và vẽ cặp hình đó cùng tâm phối cảnh vào vở.
Phương pháp giải:
Dựa vào khái niệm hình đồng dạng, hình đồng dạng phối cảnh
Lời giải chi tiết:
Cặp hình 1, 2 là cặp hình đồng dạng.
Cặp hình 2 là hình đồng dạng phối cảnh.
Video hướng dẫn giải
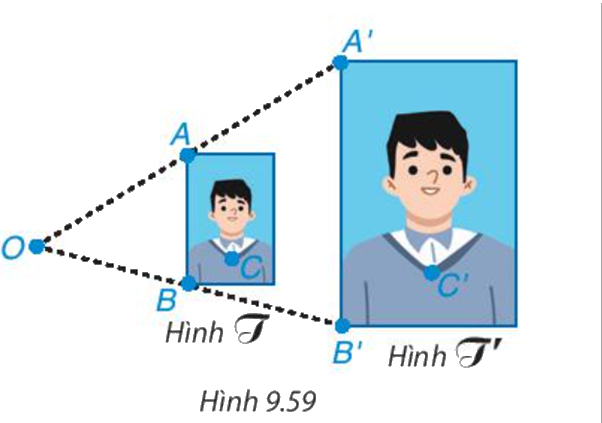
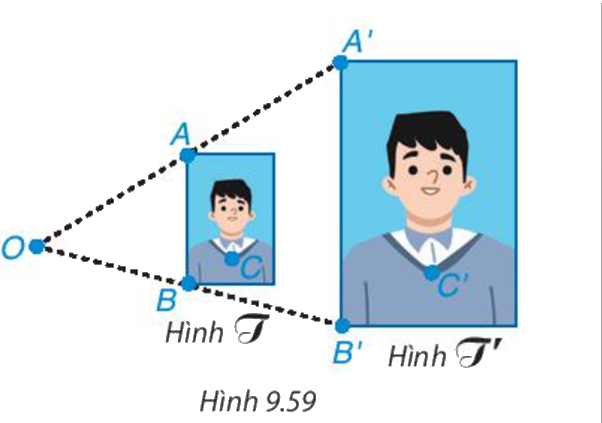
Hình 9.59 là hai bức hình chân dung của mội cậu bé với kích thước 2 x 3 (hình T) và 4 x 6 (hình T') được đặt cạnh nhau theo chiều thẳng đứng. Ta thấy các đường thẳng AA', BB' nối các điểm tương ứng trên hai bức chân dung cùng đi qua một điểm O. Dùng thước thẳng, em hãy kiểm tra xem một đường thẳng nối hai điểm tương ứng tuỳ ý trên hai hình (ví dụ C và C') có đi qua điểm O không?
Ta cũng có nói hình T' là hình phóng to của hình T với tỉ số 6 : 3 = 2, hình T là hình thu nhỏ của hình T' với tỉ số 3:6 = \(\frac{1}{2}\)
Phương pháp giải:
Quan sát hình 9.59
Lời giải chi tiết:
Một đường thẳng nối hai điểm tương ứng tùy ý trên hai hình có đi qua O
Video hướng dẫn giải
Lấy điểm O và vẽ tam giác A'B'C' như Hình 9.58. Trên các tia OA', OB', OC', lấy các điểm A, B, C sao cho OA = 2OA', OB = 2OB', OC = 2OC'
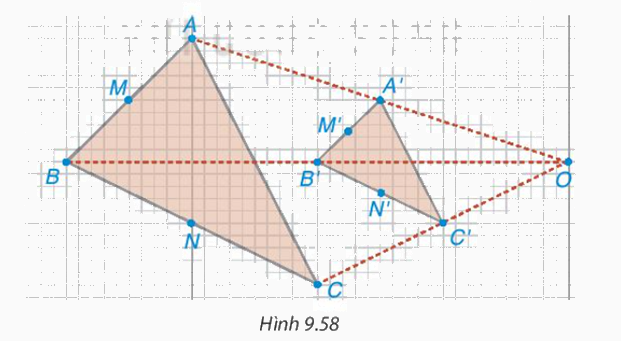
- Hãy giải thích vì sao ΔABC ∽ ΔA'B'C' với tỉ số đồng dạng bằng 2
- Dùng thước thẳng, em hãy kiểm tra xem đường thẳng MM', NN' nối các trung điểm có đi qua O không?
Trong Hình 9.58, ta nói tam giác ABC là hình phóng to (2 lần) của tam giác A'B'C' và tam giác A'B'C' là hình thu nhỏ (2 lần) của tam giác ABC
Phương pháp giải:
Vì ΔOA'B' ∽ ΔOAB (c.g.c) và ΔOB'C' ∽ ΔOBC(c.g.c) nên ΔABC ∽ ΔA'B'C' (c.g.c)
Lời giải chi tiết:
- Có \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOA'B' ∽ ΔOAB (c.g.c)
- Có \(\frac{{OC'}}{{OC}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOB'C' ∽ ΔOBC(c.g.c)
=> ΔABC ∽ ΔA'B'C' (c.g.c)
- Đường thẳng có đi qua O
Video hướng dẫn giải
Hình 9.59 là hai bức hình chân dung của mội cậu bé với kích thước 2 x 3 (hình T) và 4 x 6 (hình T') được đặt cạnh nhau theo chiều thẳng đứng. Ta thấy các đường thẳng AA', BB' nối các điểm tương ứng trên hai bức chân dung cùng đi qua một điểm O. Dùng thước thẳng, em hãy kiểm tra xem một đường thẳng nối hai điểm tương ứng tuỳ ý trên hai hình (ví dụ C và C') có đi qua điểm O không?
Ta cũng có nói hình T' là hình phóng to của hình T với tỉ số 6 : 3 = 2, hình T là hình thu nhỏ của hình T' với tỉ số 3:6 = \(\frac{1}{2}\)
Phương pháp giải:
Quan sát hình 9.59
Lời giải chi tiết:
Một đường thẳng nối hai điểm tương ứng tùy ý trên hai hình có đi qua O
Video hướng dẫn giải
Theo em, hai hình tam giác bằng nhau có phải là hai hình đồng dạng phối cảnh không?
Phương pháp giải:
Dựa vào khái niệm hình đồng dạng, hình đồng dạng phối cảnh.
Lời giải chi tiết:
Hai tam giác bằng nhau không phải là hình đồng dạng phối cảnh
Video hướng dẫn giải
Trong những cặp hình dưới đây (H.9.70), cặp hình nào là hai hình đồng dạng? Hãy chỉ ra một cặp hình đồng dạng phối cảnh và vẽ cặp hình đó cùng tâm phối cảnh vào vở.
Phương pháp giải:
Dựa vào khái niệm hình đồng dạng, hình đồng dạng phối cảnh
Lời giải chi tiết:
Cặp hình 1, 2 là cặp hình đồng dạng.
Cặp hình 2 là hình đồng dạng phối cảnh.
Video hướng dẫn giải
Vuông: Tớ nghĩ là hai hình vuông bất kì đều đồng dạng với nhau
Tròn: Tớ nghĩ hai hình tam giác đều bất kì đồng dạng phối cảnh với nhau
Theo em, bạn nào nói đúng, bạn nào nói sai? Cho biết ý kiến của em?
Phương pháp giải:
Dựa vào khái niệm hình đồng dạng, hình đồng dạng phối cảnh
Lời giải chi tiết:
Theo em, bạn Vuông nói đúng, bạn tròn nói sai
Chương trình Toán 8 tập 2 Kết nối tri thức tập trung vào việc củng cố và mở rộng các kiến thức về hình học và đại số đã học ở lớp 6 và 7. Các bài tập trang 104, 105, 106, 107 thuộc chương trình này, thường xoay quanh các chủ đề như tứ giác, hình bình hành, hình chữ nhật, hình thoi, hình vuông, và các tính chất của chúng. Việc nắm vững các định nghĩa, định lý và phương pháp chứng minh là vô cùng quan trọng để giải quyết các bài tập này một cách hiệu quả.
Bài tập: Cho tứ giác ABCD có AB = CD và AD = BC. Chứng minh rằng tứ giác ABCD là hình bình hành.
Lời giải:
Xét hai tam giác ABD và CDB, ta có:
Do đó, tam giác ABD = tam giác CDB (c-c-c). Suy ra ∠ABD = ∠CDB và ∠ADB = ∠CBD. Vì ∠ABD = ∠CDB nên AB // CD. Tương tự, vì ∠ADB = ∠CBD nên AD // BC. Vậy tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Hy vọng với những hướng dẫn chi tiết và lời giải bài tập trên, các em học sinh sẽ học tốt môn Toán 8 tập 2 Kết nối tri thức. Chúc các em thành công!