Bài 7.35 trang 54 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.35 này, giúp các em học sinh nắm vững phương pháp giải và tự tin hơn trong các bài kiểm tra.
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng
Đề bài
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y=x và y=−x+2
a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ
b) Tìm giao điểm A của hai đường thẳng đã cho
c) Gọi B là giao điểm của đường thẳng y=−x+2 và trục Ox. Chứng minh tam giác OAB vuông tại A, tức hai đường thẳng y=x và y=−x+2 vuông góc với nhau
d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Vẽ hai đường thẳng y = x và y = −x + 2 trên mặt phẳng tọa độ bằng cách xác định hai điểm thuộc mỗi đường thẳng.
b) Quan sát đồ thị hàm số y = x và y = 0x + 2 xác định tọa độ điểm A là giao điểm của hai đường thẳng đã cho.
c) Lấy C là giao điểm của đường thẳng y = -x + 2 và trục Oy, chứng minh tam giác OBC vuông cân tại O.
Chứng minh AB = AC => \(OA \bot AB\) hay tam giác OAB vuông cân tại A.
d) Xác định hệ số góc của hai đường thẳng đã cho và tính tích của chúng
Lời giải chi tiết
a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\
* Xét đường thẳng y = -x + 2
Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2
Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2
Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2)
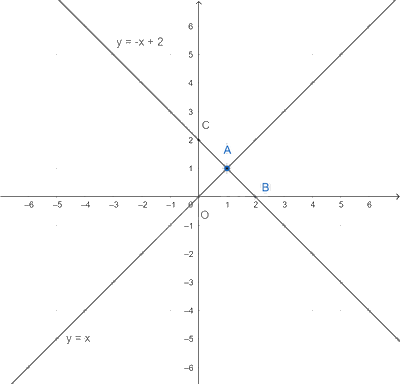
b) Gọi A(x0; y0) là giao điểm của hai đường thẳng đã cho. Khi đó, cả hai đường thẳng đã cho đồng thời đi qua điểm A, do đó, ta có:
y0 = x0 và y0 = -x0 + 2, suy ra x0 = −x0 + 2, hay x0 = 1.
Vậy hai đường thẳng đã cho cắt nhau tại điểm A(1;1).
c) Giao điểm của đường thẳng y = -x + 2 và trục Ox là B(2; 0). Suy ra OB = 2.
Vì OA là đường chéo của hình vuông có cạnh bằng 1 nên suy ra OA = \(\sqrt 2 \).
Vì AB là đường chéo của hình vuông có cạnh bằng 1 nên suy ra AB = \(\sqrt 2 \).
Ta có: \(O{A^2} + A{B^2} = {\left( {\sqrt 2 } \right)^2} + {\left( {\sqrt 2 } \right)^2} = 4;O{B^2} = 4.\)
Do đó OA2 + AB2 = OB2, suy ra tam giác OAB vuông tại A (theo định lí Pythagore đảo).
d)
Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = - x + 1 có hệ số góc bằng -1
Tích của hai hệ số góc bằng -1
Bài 7.35 trang 54 SGK Toán 8 tập 2 yêu cầu học sinh chứng minh một tính chất liên quan đến hình thang cân. Để giải bài này, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Nội dung bài toán: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng EA = EB.
Lời giải:
Xét tam giác ADE và tam giác BCE:
Do đó, tam giác ADE đồng dạng với tam giác BCE (g-g).
Suy ra: EA/EB = AD/BC
Mà AD = BC (tính chất hình thang cân) nên EA/EB = 1
Vậy EA = EB (đpcm).
Phân tích cách giải:
Để chứng minh EA = EB, chúng ta đã sử dụng phương pháp chứng minh hai tam giác đồng dạng. Việc nhận ra hai góc bằng nhau (∠DAE = ∠CBE và ∠AED = ∠BEC) và sử dụng tính chất hình thang cân (AD = BC) là chìa khóa để giải quyết bài toán này.
Mở rộng:
Bài toán này có thể được mở rộng bằng cách yêu cầu học sinh chứng minh các tính chất khác của hình thang cân, ví dụ như chứng minh hai đường chéo bằng nhau. Ngoài ra, học sinh cũng có thể áp dụng kiến thức về tam giác đồng dạng để giải các bài toán liên quan đến hình thang nói chung.
Bài tập tương tự:
Kết luận:
Bài 7.35 trang 54 SGK Toán 8 tập 2 là một bài tập điển hình về hình thang cân. Việc nắm vững các kiến thức cơ bản và phương pháp giải quyết bài toán sẽ giúp học sinh tự tin hơn trong việc học tập môn Toán.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn giải bài tập này, các em học sinh sẽ hiểu rõ hơn về kiến thức hình học và đạt kết quả tốt trong các bài kiểm tra.
Các kiến thức liên quan:
Lưu ý:
Khi giải bài tập hình học, học sinh nên vẽ hình chính xác và ghi chú các yếu tố đã biết để dễ dàng theo dõi và tìm ra hướng giải quyết.
Ngoài ra, học sinh cũng nên luyện tập thêm các bài tập tương tự để củng cố kiến thức và rèn luyện kỹ năng giải toán.