Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 64, 65 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
Video hướng dẫn giải
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
Phương pháp giải:
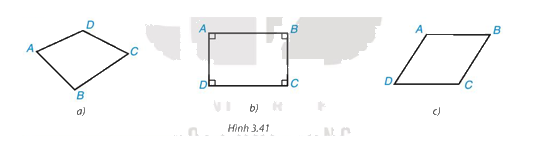
Quan sát hình 3.41
Lời giải chi tiết:
Tứ giác ABCD trong Hình 3.41b là hình chữ nhật vì có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
Tứ giác ABCD trong Hình 3.41a và Hình 3.41c không phải là hình chữ nhật vì không có 4 góc vuông.
Video hướng dẫn giải
Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Ta có tính chất sau đây về đường chéo của hình chữ nhật.
Phương pháp giải:
Giả sử có hình chữ nhật ABCD.
Chứng minh hình chữ nhật ABCD có AD // BC; AB // CD nên ABCD là hình bình hành.
Chứng minh hình chữ nhật ABCD là hình thang.
Lời giải chi tiết:
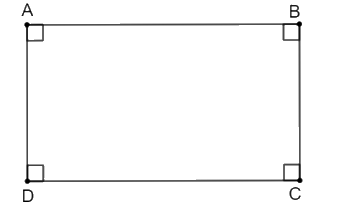
Ta đặt hình chữ nhật ABCD như hình vẽ.
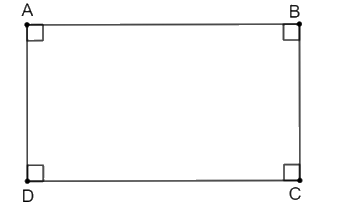
Vì ABCD là hình chữ nhật .
Ta có: AB ⊥ AD; AB ⊥ BC suy ra AD // BC.
AB ⊥ AD; CD ⊥ AD suy ra AB // CD.
• Vì ABCD là hình chữ nhật nên AD // BC; AB // CD
Suy ra ABCD cũng là hình bình hành.
• Vì ABCD là hình chữ nhật nên AB // CD suy ra ABCD cũng là hình thang.
Hình thang ABCD có AD = BC.
Do đó ABCD cũng là hình thang cân.
Vì ABCD vừa là hình bình hành vừa là hình thang cân nên có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Video hướng dẫn giải
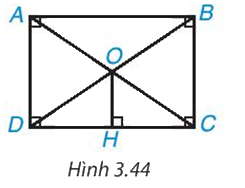
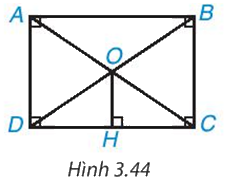
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
Phương pháp giải:
Xét tam giác ODC là tam giác cân có OH là đường cao nên OH cùng là trung tuyến. Do đó: CH = HD.
Lời giải chi tiết:
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.
Video hướng dẫn giải
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
Phương pháp giải:
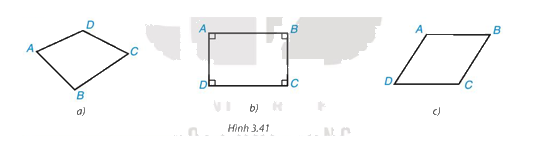
Quan sát hình 3.41
Lời giải chi tiết:
Tứ giác ABCD trong Hình 3.41b là hình chữ nhật vì có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
Tứ giác ABCD trong Hình 3.41a và Hình 3.41c không phải là hình chữ nhật vì không có 4 góc vuông.
Video hướng dẫn giải
Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Ta có tính chất sau đây về đường chéo của hình chữ nhật.
Phương pháp giải:
Giả sử có hình chữ nhật ABCD.
Chứng minh hình chữ nhật ABCD có AD // BC; AB // CD nên ABCD là hình bình hành.
Chứng minh hình chữ nhật ABCD là hình thang.
Lời giải chi tiết:
Ta đặt hình chữ nhật ABCD như hình vẽ.
Vì ABCD là hình chữ nhật .
Ta có: AB ⊥ AD; AB ⊥ BC suy ra AD // BC.
AB ⊥ AD; CD ⊥ AD suy ra AB // CD.
• Vì ABCD là hình chữ nhật nên AD // BC; AB // CD
Suy ra ABCD cũng là hình bình hành.
• Vì ABCD là hình chữ nhật nên AB // CD suy ra ABCD cũng là hình thang.
Hình thang ABCD có AD = BC.
Do đó ABCD cũng là hình thang cân.
Vì ABCD vừa là hình bình hành vừa là hình thang cân nên có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Video hướng dẫn giải
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
Phương pháp giải:
Xét tam giác ODC là tam giác cân có OH là đường cao nên OH cùng là trung tuyến. Do đó: CH = HD.
Lời giải chi tiết:
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.
Mục 1 trang 64, 65 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép toán với đa thức. Đây là một phần quan trọng trong chương trình học Toán 8, giúp học sinh chuẩn bị cho các bài học tiếp theo. Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết các bài toán phức tạp một cách dễ dàng hơn.
Mục 1 bao gồm các nội dung sau:
Bài tập 1 yêu cầu thực hiện các phép tính cộng, trừ đa thức. Để giải bài tập này, học sinh cần nắm vững quy tắc cộng, trừ các đơn thức đồng dạng và các tính chất của phép cộng, trừ.
Ví dụ:
Tính: (3x2 - 5x + 2) + (x2 + 2x - 1)
Giải:
(3x2 - 5x + 2) + (x2 + 2x - 1) = 3x2 - 5x + 2 + x2 + 2x - 1 = (3x2 + x2) + (-5x + 2x) + (2 - 1) = 4x2 - 3x + 1
Bài tập 2 yêu cầu thực hiện các phép tính nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững quy tắc nhân, chia các đơn thức và đa thức, cũng như các tính chất của phép nhân, chia.
Ví dụ:
Tính: (2x + 1)(x - 3)
Giải:
(2x + 1)(x - 3) = 2x(x - 3) + 1(x - 3) = 2x2 - 6x + x - 3 = 2x2 - 5x - 3
Bài tập 3 yêu cầu giải các bài toán thực tế liên quan đến đa thức. Để giải bài tập này, học sinh cần vận dụng kiến thức đã học để xây dựng phương trình và giải phương trình đó.
Ví dụ:
Một hình chữ nhật có chiều dài là (x + 5) cm và chiều rộng là (x - 2) cm. Tính diện tích của hình chữ nhật đó.
Giải:
Diện tích của hình chữ nhật là: (x + 5)(x - 2) = x2 - 2x + 5x - 10 = x2 + 3x - 10 (cm2)
Việc giải các bài tập trong Mục 1 trang 64, 65 SGK Toán 8 tập 1 - Kết nối tri thức là một bước quan trọng trong quá trình học Toán 8. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn học này.
| Phép toán | Công thức |
|---|---|
| Cộng đa thức | (A + B) = A + B (với A, B là các đa thức) |
| Trừ đa thức | (A - B) = A - B (với A, B là các đa thức) |
| Nhân đa thức | (A * B) = A * B (với A, B là các đa thức) |
| Chia đa thức | (A / B) = A / B (với A, B là các đa thức) |