Bài học này cung cấp kiến thức nền tảng về đường phân giác của tam giác, một khái niệm quan trọng trong hình học lớp 8. Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất và ứng dụng của đường phân giác trong giải toán.
Nội dung bài học được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể, giúp học sinh nắm bắt kiến thức một cách nhanh chóng và hiệu quả. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Đường phân giác có tính chất gì?
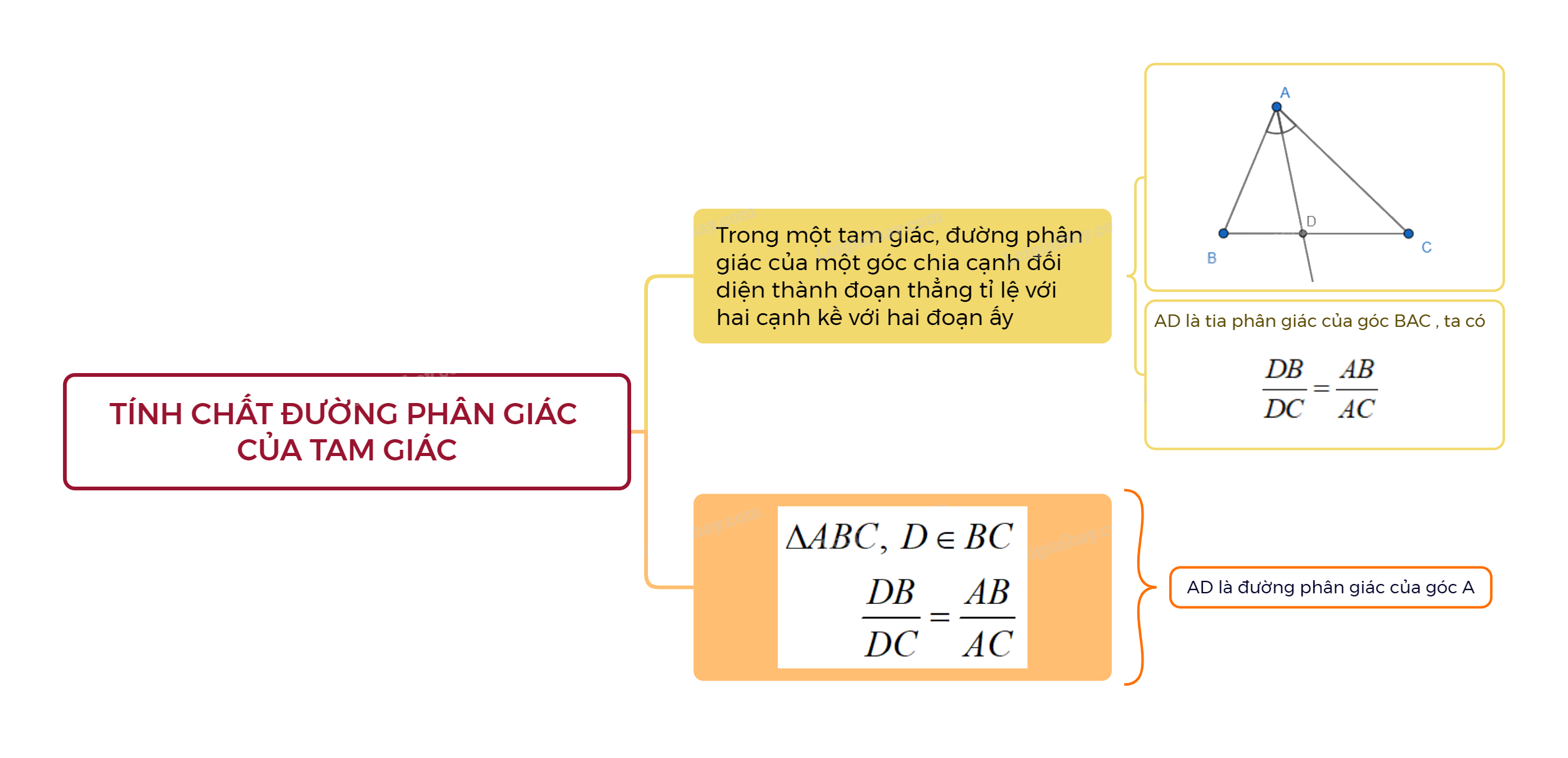
Tính chất của đường phân giác
Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
Chú ý: Trong tam giác ABC, nếu D là điểm thuộc đoạn thẳng BC và thỏa mãn \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) thì AD là đường phân giác của góc A
Ví dụ:
AD là tia phân giác của \(\widehat {BAC}\), ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\)
Đường phân giác của một tam giác là đoạn thẳng nối đỉnh của tam giác với điểm chia cạnh đối diện thành hai đoạn thẳng bằng nhau. Nói cách khác, đường phân giác chia góc của tam giác thành hai góc bằng nhau.
Trong tam giác ABC, đường thẳng AD (với D nằm trên BC) được gọi là đường phân giác của góc A nếu ∠BAD = ∠CAD.
Tính chất quan trọng nhất của đường phân giác là:
Chứng minh tính chất 1 có thể thực hiện bằng cách sử dụng định lý Thales hoặc bằng cách xét hai tam giác có chung chiều cao và diện tích.
Tính chất đường phân giác được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác, đặc biệt là các bài toán về tỉ lệ thức và tính độ dài đoạn thẳng.
Cho tam giác ABC có AB = 6cm, AC = 9cm, BC = 10cm. AD là đường phân giác của góc BAC (D thuộc BC). Tính độ dài BD và CD.
Giải:
Áp dụng tính chất đường phân giác, ta có:
AB/AC = BD/CD => 6/9 = BD/CD => BD/CD = 2/3
Mà BD + CD = BC = 10cm
Suy ra BD = (2/5) * 10 = 4cm và CD = (3/5) * 10 = 6cm
Cho tam giác ABC, đường phân giác AD chia BC thành hai đoạn BD = 3cm và CD = 5cm. Nếu AB = 4cm, tính độ dài AC.
Giải:
Áp dụng tính chất đường phân giác, ta có:
AB/AC = BD/CD => 4/AC = 3/5 => AC = (4 * 5)/3 = 20/3 cm
Để củng cố kiến thức về tính chất đường phân giác, bạn có thể thực hành giải các bài tập sau:
Khi áp dụng tính chất đường phân giác, cần chú ý đến điều kiện: điểm D phải nằm trên cạnh BC. Ngoài ra, cần phân biệt rõ giữa đường phân giác, đường trung tuyến và đường cao của tam giác.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết tính chất đường phân giác của tam giác. Chúc bạn học tốt!