Bài 3.3 trang 50 SGK Toán 8 tập 1 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để xác định mối quan hệ giữa các góc và giải quyết các bài toán liên quan.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.3 trang 50 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
Đề bài
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
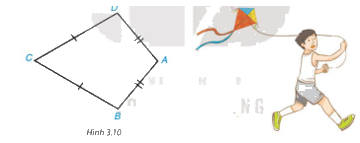
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Tính các góc B, D biết rằng \(\widehat A\)=100°,\(\widehat C\)=60°
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí tổng các góc trong một tứ giác bằng \(360^0\)
Lời giải chi tiết
a) Nối AC, BD (như hình vẽ
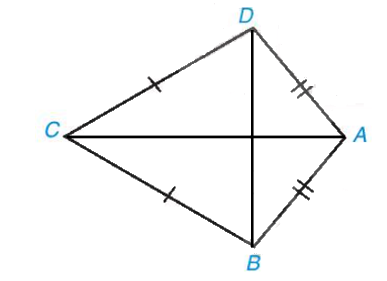
Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
b) Gọi I là giao điểm của AC và BD.
Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.
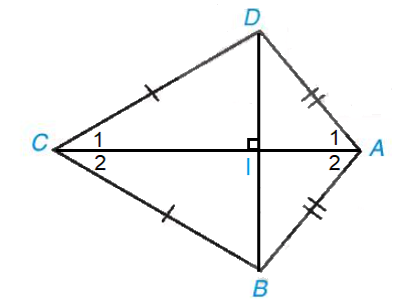
• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)
Nên AI cũng là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay \(\widehat {{A_1}} = \widehat {{A_2}}\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {B{\rm{D}}A}:2 = {100^o}:2 = {50^o}\)
• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)
Nên CI cũng là tia phân giác của \(\widehat {BC{\rm{D}}}\) hay \(\widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra \(\widehat {{C_1}} = \widehat {{C_2}} = \widehat {BC{\rm{D}}}:2 = {60^o}:2 = {30^o}\)
• Xét tam giác ACD có: \(\widehat {{A_1}} + \widehat {{C_1}} + \widehat {A{\rm{D}}C} = {180^o}\) (định lí tổng ba góc trong một tam giác).
Hay 50°+30°+\(\widehat {A{\rm{D}}C}\)=180°
Suy ra \(\widehat {A{\rm{D}}C}\)=180°−50°−30°=100°
Xét tứ giác ABCD có:
\(\widehat {BA{\rm{D}}} + \widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {A{\rm{D}}C} = {360^o}\)(định lí tổng bốn góc của một tứ giác).
Hay 100°+\(\widehat {ABC}\)+60°+100°=360°
Suy ra \(\widehat {ABC}\)+260°=360o
Do đó \(\widehat {ABC}\)=360°−260°=100o
Vậy \(\widehat {ABC}\)=100° ;\(\widehat {A{\rm{D}}C}\)=100°
Bài 3.3 trang 50 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Để giải bài tập này, học sinh cần nắm vững các khái niệm sau:
Khi một đường thẳng cắt hai đường thẳng song song, các góc so le trong bằng nhau, các góc đồng vị bằng nhau, và các góc trong cùng phía bù nhau.
Đề bài: (Xem lại đề bài trong SGK Toán 8 tập 1 - Kết nối tri thức trang 50)
Giải:
(Giải thích chi tiết từng bước giải bài tập, bao gồm cả việc vẽ hình minh họa nếu cần thiết. Ví dụ, nếu đề bài yêu cầu chứng minh hai đường thẳng song song, cần chỉ ra các góc so le trong bằng nhau, hoặc các góc đồng vị bằng nhau, hoặc các góc trong cùng phía bù nhau. Giải thích rõ ràng lý do tại sao lại sử dụng phương pháp đó.)
Để hiểu rõ hơn về cách giải bài 3.3, chúng ta cùng xem xét một ví dụ minh họa sau:
Ví dụ: Cho hình vẽ, biết góc A1 = 60 độ. Tính góc B1.
(Vẽ hình minh họa và giải thích cách tính góc B1 dựa trên kiến thức về góc so le trong, đồng vị, hoặc trong cùng phía.)
Ngoài ra, các em có thể tự giải các bài tập tương tự sau để rèn luyện kỹ năng:
Kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, và hàng hải. Ví dụ, trong kiến trúc, các kiến trúc sư sử dụng kiến thức này để thiết kế các công trình đảm bảo tính thẩm mỹ và độ bền vững. Trong hàng hải, các thủy thủ sử dụng kiến thức này để xác định hướng đi của tàu.
Bài 3.3 trang 50 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.