Phương trình bậc nhất một ẩn là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 8 - Kết nối tri thức. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết Phương trình bậc nhất một ẩn, cùng với các bài tập vận dụng đa dạng để giúp bạn học tập hiệu quả.
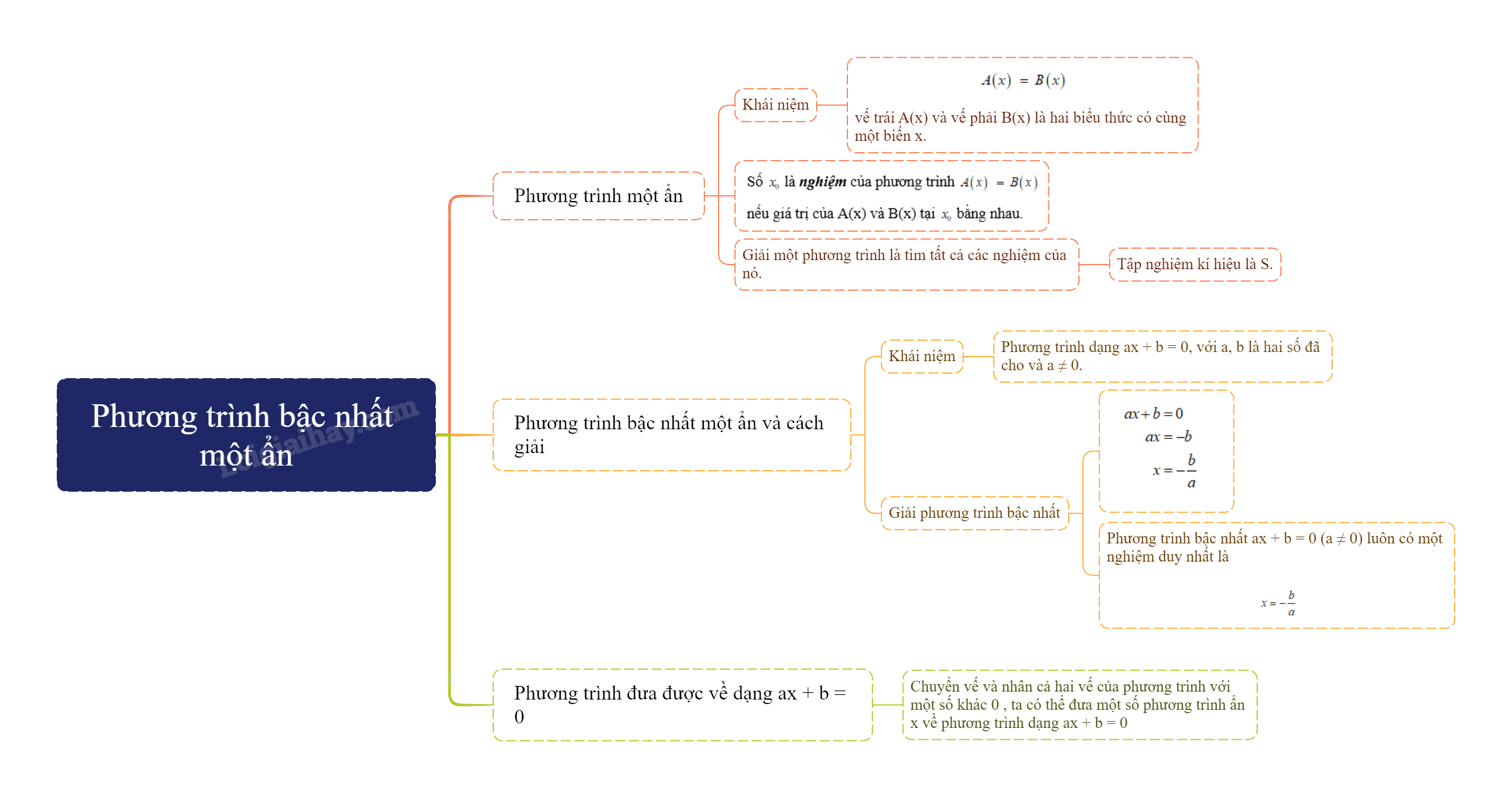
Phương trình bậc nhất một ẩn là gì?
1. Phương trình một ẩn
Khái niệm:
Một phương trình với ẩn x có dạng \(A\left( x \right){\rm{ }} = {\rm{ }}B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức có cùng một biến x.
Ví dụ: \(3x{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}2x{\rm{ }} + {\rm{ }}3;{\rm{ }}3x{\rm{ }} = {\rm{ }}5\) là các phương trình ẩn x.
Số \({x_0}\) là nghiệm của phương trình \(A\left( x \right){\rm{ }} = {\rm{ }}B\left( x \right)\)nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.
Ví dụ: \(x{\rm{ }} = {\rm{ }}2\) là nghiệm của phương trình \(2x{\rm{ }} = {\rm{ }}x{\rm{ }} + {\rm{ }}2\) vì thay \(x{\rm{ }} = {\rm{ }}2\) vào phương trình, ta được 2.2 = 2 + 2
Giải một phương trình là tìm tất cả các nghiệm của nó.
Chú ý: Tập hợp tất cả các nghiệm của một phương trình được gọi là tập nghiệm của phương trình đó và kí hiệu là S.
Ví dụ: Giải phương trình: \(3x + 6 = 0\)
Ta có: \(3x + 6 = 0 \Leftrightarrow 3x = - 6 \Leftrightarrow x = - 2\)
Vậy tập nghiệm của phương trình là S = {-2}
2. Phương trình bậc nhất một ẩn và cách giải
Khái niệm: Phương trình dạng ax + b = 0, với a, b là hai số đã cho và \(a \ne 0\), được gọi là phương trình bậc nhất một ẩn x.
Cách giải:
Phương trình bậc nhất ax + b = 0 (\(a \ne 0\)) được giải như sau:
\(\begin{array}{c}ax + b = 0\\ax = - b\\x = - \frac{b}{a}\end{array}\)
Phương trình bậc nhất ax + b = 0 (\(a \ne 0\)) luôn có một nghiệm duy nhất là \(x = - \frac{b}{a}\).
Ví dụ: Giải phương trình: \(3x + 11 = 0\)
Ta có: \(3x + 11 = 0 \Leftrightarrow 3x = - 11 \Leftrightarrow x = - \frac{{11}}{3}\)
Vậy nghiệm của phương trình là \(x = - \frac{{11}}{3}\).
3. Phương trình đưa được về dạng ax + b = 0
Bằng cách chuyển vế và nhân cả hai vế của phương trình với một số khác 0, ta có thể đưa một số phương trình ẩn x về phương trình dạng ax + b = 0 và do đó có thể giải được chúng.
Ví dụ: Giải phương trình: \(7x{\rm{ }}-{\rm{ }}\left( {2x{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}5\left( {x{\rm{ }}-{\rm{ }}2} \right)\)
\(\begin{array}{c}11x{\rm{ }}-{\rm{ }}\left( {2x{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ 6}}\left( {x{\rm{ }}-{\rm{ }}2} \right)\\11x - 2x - 3 = 6x - 12\\11x - 2x - 6x = - 12 + 3\\3x = - 9\\x = \frac{{ - 9}}{3}\\x = - 3\end{array}\)
Vậy nghiệm của phương trình là x = -3
Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0, trong đó x là ẩn số, a và b là các hệ số với a ≠ 0. Hiểu rõ định nghĩa này là bước đầu tiên để làm chủ chủ đề này.
Như đã đề cập, phương trình bậc nhất một ẩn có dạng tổng quát là ax + b = 0 (với a ≠ 0). Ẩn số là đại lượng chưa biết, cần tìm giá trị để thỏa mãn phương trình. Hệ số a xác định bậc của phương trình (trong trường hợp này là bậc nhất). Hệ số b là hằng số.
Để giải phương trình bậc nhất một ẩn, chúng ta thực hiện các bước sau:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Vậy nghiệm của phương trình là x = 3.
Ví dụ 2: Giải phương trình -3x - 7 = 8
Vậy nghiệm của phương trình là x = -5.
Các bài tập về phương trình bậc nhất một ẩn thường gặp các dạng sau:
Phương trình bậc nhất một ẩn được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Để nắm vững kiến thức về phương trình bậc nhất một ẩn, bạn nên luyện tập thường xuyên các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, đa dạng, được phân loại theo mức độ khó để giúp bạn củng cố kiến thức một cách hiệu quả.
Hãy bắt đầu hành trình chinh phục môn Toán 8 với chúng tôi ngay hôm nay!