Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 79, 80 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải này với mục tiêu giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Tìm các độ dài x, y trong Hình 4.6.
Video hướng dẫn giải
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).
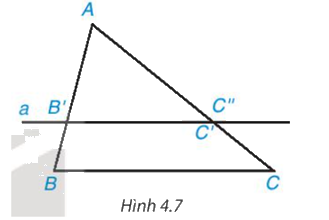
• So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.
• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?
Phương pháp giải:
Áp dụng định lí Thalès vào ∆ABC
Lời giải chi tiết:
• Ta có \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{6}{9} = \dfrac{2}{3}\)
Do đó \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\)
• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.
Áp dụng định lí Thalès vào ∆ABC, ta có:
\(\dfrac{{AB'}}{{AB}} = \dfrac{{AC''}}{{AC}}\) hay \(\dfrac{4}{6} = \dfrac{{AC''}}{9}\)
Suy ra: \(AC'' = \dfrac{{4.9}}{6} = 6\)(cm).
Vậy AC’’ = 6 cm.
• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.
Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.
Do đó, hai điểm C’, C’’ trùng nhau.
Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.
Video hướng dẫn giải
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
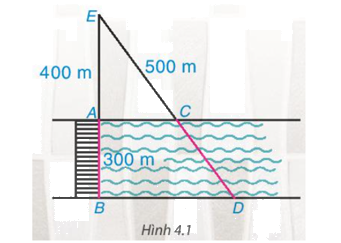
Phương pháp giải:
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès
Lời giải chi tiết:
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m
Video hướng dẫn giải
Tìm các độ dài x, y trong Hình 4.6.
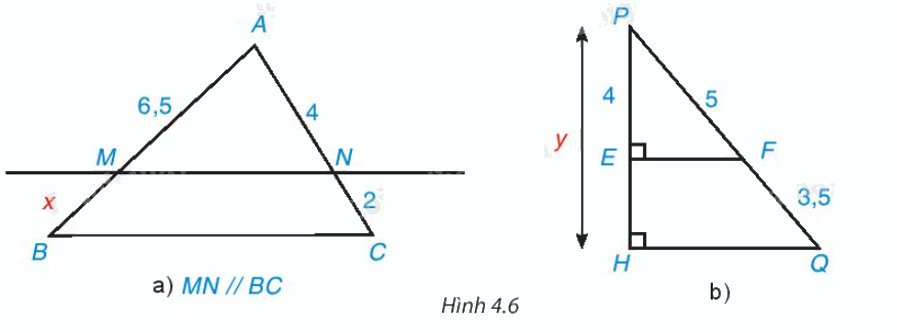
Phương pháp giải:
Áp dụng định lí Thalès
Lời giải chi tiết:
a) Áp dụng định lí Thalès vào ∆ABC, ta có:
\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{{6,5}}{x} = \dfrac{4}{2}\)
Suy ra \(x = \dfrac{{6,5.2}}{4} = 3,25\) (đvđd).
Vậy x = 3,25 (đvđd).
b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).
Áp dụng định lí Thalès vào ∆PHQ, ta có:
\(\dfrac{{PE}}{{PH}} = \dfrac{{PF}}{{PQ}}\) hay \(\dfrac{4}{y} = \dfrac{5}{{8,5}}\)
Suy ra \(y = \dfrac{{4.8,5}}{5} = 6,8\) (đvđd).
Vậy y = 6,8 (đvđd)
Video hướng dẫn giải
Tìm các độ dài x, y trong Hình 4.6.
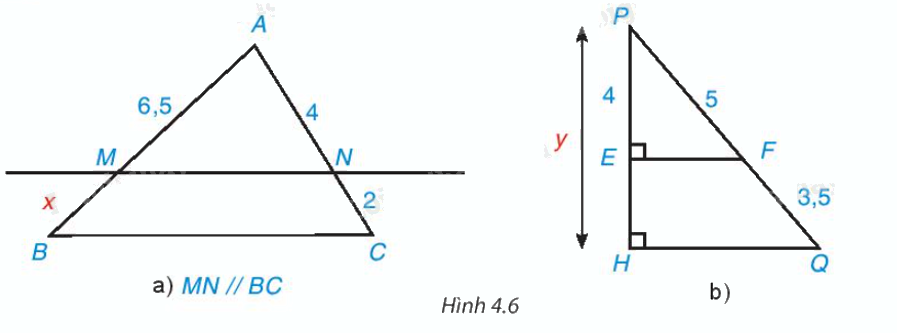
Phương pháp giải:
Áp dụng định lí Thalès
Lời giải chi tiết:
a) Áp dụng định lí Thalès vào ∆ABC, ta có:
\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{{6,5}}{x} = \dfrac{4}{2}\)
Suy ra \(x = \dfrac{{6,5.2}}{4} = 3,25\) (đvđd).
Vậy x = 3,25 (đvđd).
b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).
Áp dụng định lí Thalès vào ∆PHQ, ta có:
\(\dfrac{{PE}}{{PH}} = \dfrac{{PF}}{{PQ}}\) hay \(\dfrac{4}{y} = \dfrac{5}{{8,5}}\)
Suy ra \(y = \dfrac{{4.8,5}}{5} = 6,8\) (đvđd).
Vậy y = 6,8 (đvđd)
Video hướng dẫn giải
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).
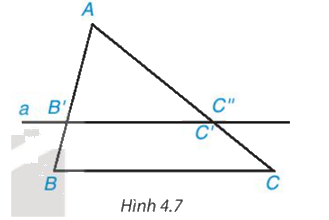
• So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.
• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?
Phương pháp giải:
Áp dụng định lí Thalès vào ∆ABC
Lời giải chi tiết:
• Ta có \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{6}{9} = \dfrac{2}{3}\)
Do đó \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\)
• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.
Áp dụng định lí Thalès vào ∆ABC, ta có:
\(\dfrac{{AB'}}{{AB}} = \dfrac{{AC''}}{{AC}}\) hay \(\dfrac{4}{6} = \dfrac{{AC''}}{9}\)
Suy ra: \(AC'' = \dfrac{{4.9}}{6} = 6\)(cm).
Vậy AC’’ = 6 cm.
• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.
Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.
Do đó, hai điểm C’, C’’ trùng nhau.
Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.
Video hướng dẫn giải
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
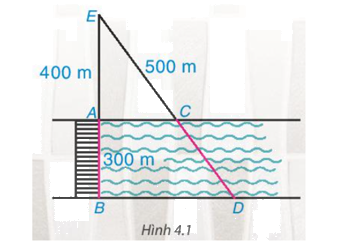
Phương pháp giải:
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès
Lời giải chi tiết:
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m
Mục 2 trang 79, 80 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc vận dụng các kiến thức về hình hộp chữ nhật và hình lập phương để giải các bài toán thực tế. Các bài tập thường yêu cầu tính thể tích, diện tích bề mặt, hoặc xác định các yếu tố của hình. Để giải quyết hiệu quả các bài toán này, học sinh cần nắm vững các công thức và phương pháp sau:
Ngoài ra, học sinh cần rèn luyện kỹ năng đọc kỹ đề bài, xác định đúng các yếu tố cần tìm, và lựa chọn phương pháp giải phù hợp.
Lời giải:
Áp dụng công thức tính thể tích hình hộp chữ nhật, ta có:
V = 5cm . 4cm . 3cm = 60cm3
Vậy thể tích của hình hộp chữ nhật là 60cm3.
Lời giải:
Áp dụng công thức tính thể tích hình lập phương, ta có:
V = 2cm3 = 8cm3
Vậy thể tích của hình lập phương là 8cm3.
Lời giải:
Áp dụng công thức tính thể tích hình hộp chữ nhật, ta có:
V = 1.2m . 0.8m . 1m = 0.96m3
Vậy thể tích của bể nước là 0.96m3.
Lời giải:
Áp dụng công thức tính diện tích bề mặt hình lập phương, ta có:
S = 6a2 = 150cm2
Suy ra a2 = 150cm2 / 6 = 25cm2
Vậy a = √25cm2 = 5cm
Vậy cạnh của hình lập phương là 5cm.
Để hiểu sâu hơn về các khái niệm và công thức liên quan đến hình hộp chữ nhật và hình lập phương, các em có thể tham khảo thêm các bài tập sau:
Ngoài ra, các em có thể tìm kiếm thêm các tài liệu học tập trực tuyến, video bài giảng, hoặc tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng giải bài tập.
Để học tốt môn Toán 8, các em cần:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán 8!