Bài 3.17 trang 61 SGK Toán 8 tập 1 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.17, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình bình hành ABCD.
Đề bài
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành;
b) EF = AD, AF = EC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh tứ giác tứ giác AEFD, AECF có cặp cạnh đối song song và bằng nhau nên tứ giác AEFD, AECF là hình bình hành.
b) Sử dụng tính chất của hình bình hành để chứng minh EF = AD; AF = EC.
Lời giải chi tiết
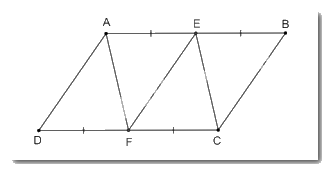
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
• Xét tứ giác AEFD có:
AE // DF (vì AB // CD);
AE = DF (chứng minh trên)
Do đó tứ giác AEFD là hình bình hành.
• Xét tứ giác AECF có:
AE // CF (vì AB // CD);
AE = CF (chứng minh trên)
Do đó tứ giác AECF là hình bình hành.
Vậy hai tứ giác AEFD, AECF là những hình bình hành.
b) Vì tứ giác AEFD là hình bình hành nên EF = AD.
Vì tứ giác AECF là hình bình hành nên AF = EC.
Vậy EF = AD, AF = EC.
Bài 3.17 trang 61 SGK Toán 8 tập 1 yêu cầu học sinh chứng minh một tính chất liên quan đến các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Phương pháp giải bài tập này thường dựa trên việc sử dụng các tính chất trên để chứng minh các góc bằng nhau hoặc bù nhau.
Đề bài: (Xem SGK Toán 8 tập 1 - Kết nối tri thức)
Lời giải:
(Phần này sẽ chứa lời giải chi tiết của bài toán, bao gồm hình vẽ minh họa, các bước chứng minh, và giải thích rõ ràng. Ví dụ:)
a) Ta có: ∠A1 = ∠B1 (so le trong) do a // b.
b) Ta có: ∠A2 + ∠A1 = 180° (kề bù).
Mà ∠A1 = ∠B1 (cmt) nên ∠A2 + ∠B1 = 180°.
Vậy ∠A2 và ∠B1 là hai góc trong cùng phía bù nhau.
c) Tương tự, ta có thể chứng minh ∠A3 và ∠B2 là hai góc trong cùng phía bù nhau.
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa sau:
(Ví dụ minh họa với hình vẽ và lời giải chi tiết)
Ngoài ra, các em có thể tham khảo một số bài tập tương tự sau:
Khi giải các bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng, các em cần lưu ý những điều sau:
Bài 3.17 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể tự tin giải các bài tập tương tự.
| Loại góc | Tính chất |
|---|---|
| So le trong | Bằng nhau |
| Đồng vị | Bằng nhau |
| Trong cùng phía | Bù nhau |