Giải bài 4.18 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức

Bài 4.18 trang 89 SGK Toán 8 tập 1 thuộc chương 4: Các tứ giác đặc biệt. Bài tập này yêu cầu học sinh vận dụng kiến thức về hình thang cân, tính chất đường trung bình của hình thang để giải quyết. Giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 8, Toán 7, Toán 6, Toán 9, Toán 10, Toán 11, Toán 12.

Độ dài x trong Hình 4.31 bằng

Đề bài

Độ dài x trong Hình 4.31 bằng

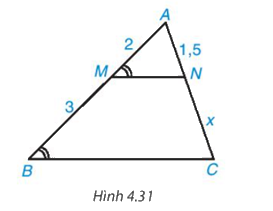
Giải bài 4.18 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức 1

A. 2,75

B. 2.

C. 2,25.

D. 3,75.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài 4.18 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức 2

Chứng minh MN // BC, áp dụng định lí Thalès vào tam giác ABC.

Lời giải chi tiết

Đáp án đúng là: C

Trong Hình 4.31 có \(\widehat {AMN} = \widehat {ABC}\) mà hai góc này ở vị trí đồng vị nên MN // BC.

Áp dụng định lí Thalès vào tam giác ABC, ta có:

\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{2}{3} = \dfrac{{1,5}}{x}\)

Suy ra \(x = \dfrac{{1,5.3}}{2} = 2,25\)

Vậy x = 2,25.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 4.18 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục giải toán 8 trên môn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 4.18 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức: Hướng dẫn chi tiết

Bài 4.18 SGK Toán 8 tập 1 - Kết nối tri thức yêu cầu chúng ta chứng minh một tính chất quan trọng của hình thang cân. Để giải bài này, học sinh cần nắm vững định nghĩa và các tính chất của hình thang cân, đặc biệt là tính chất về các góc đáy bằng nhau và các cạnh bên bằng nhau.

Đề bài:

Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng EA = EB.

Lời giải:

a) Chứng minh tam giác EAB cân tại E:

Vì ABCD là hình thang cân nên AD = BC.
Xét tam giác EAB, ta có: ∠EAB = ∠EBA (do AB // CD, ∠EAB là góc so le trong với ∠EDA, ∠EBA là góc so le trong với ∠ECB, mà ∠EDA = ∠ECB do ABCD là hình thang cân).
Do đó, tam giác EAB cân tại E (dấu hiệu nhận biết tam giác cân). Suy ra EA = EB.

b) Chứng minh ED = EC:

Vì ABCD là hình thang cân nên ∠ADC = ∠BCD.
Xét tam giác EDC, ta có: ∠EDC = ∠ECD (do ∠EDC = ∠ADC và ∠ECD = ∠BCD, mà ∠ADC = ∠BCD).
Do đó, tam giác EDC cân tại E. Suy ra ED = EC.

Phân tích và mở rộng:

Bài toán này là một ứng dụng quan trọng của các tính chất hình thang cân và tam giác cân. Việc chứng minh tam giác EAB cân tại E và tam giác EDC cân tại E là chìa khóa để giải quyết bài toán. Học sinh cần rèn luyện kỹ năng phân tích hình, vận dụng các định lý và tính chất đã học để giải quyết các bài toán tương tự.

Các dạng bài tập tương tự:

Ngoài bài 4.18, học sinh có thể gặp các bài tập tương tự liên quan đến hình thang cân, ví dụ:

Chứng minh một đường thẳng là đường trung bình của hình thang cân.
Tính độ dài các cạnh của hình thang cân khi biết một số thông tin về các cạnh và góc.
Giải các bài toán thực tế liên quan đến hình thang cân.

Lưu ý khi giải bài tập hình thang cân:

Luôn vẽ hình chính xác và đầy đủ.
Nắm vững định nghĩa và các tính chất của hình thang cân.
Vận dụng linh hoạt các định lý và tính chất đã học.
Kiểm tra lại kết quả sau khi giải xong.

Tổng kết:

Bài 4.18 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân. Việc hiểu rõ lời giải và các bước thực hiện sẽ giúp học sinh tự tin giải quyết các bài tập tương tự và nâng cao kỹ năng giải toán hình học.

Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài tập và có thêm động lực để học tập môn Toán.